
分析 (1)首先解每个不等式,两个不等式解集的公共部分就是不等式组的解集;
(2)去分母化成整式方程,解整式方程求得x的值,然后进行检验即可.
解答 解:(1)$\left\{\begin{array}{l}{5x-3<4x…①}\\{4(x-1)+3≥2x…②}\end{array}\right.$,
解①得x<3,
解②得x≥$\frac{1}{2}$.
则不等式组的解集是:$\frac{1}{2}$≤x<3;
(2)去分母,得-1=1-x-3(2-x),
去括号,得-1=1-x-6+3x,
移项,得-3x+x=1-6+1,
合并同类项,得-2x=-4,
系数化成1得x=2,
检验:当x=2时,2-x=0,则方程无解.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
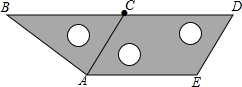 如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )
如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2$\sqrt{2}$,AC=3$\sqrt{2}$,BC=6,则⊙O的半径是( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
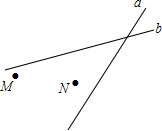 如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
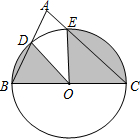 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )| A. | $\frac{64}{9}π$ | B. | $\frac{32}{9}π$ | C. | $\frac{16}{9}π$ | D. | $\frac{8}{9}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com