练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等腰三角形有一边长3cm，周长为13cm，则该等腰三角形的底边为__________cm．


    3cm．

    【考点】等腰三角形的性质；三角形三边关系．

    【分析】分3cm长的边是腰和底边两种情况进行讨论即可求解．

    【解答】解：当长是3cm的边是底边时，三边为3cm，5cm，5cm，等腰三角形成立；

    当长是3cm的边是腰时，底边长是：13﹣3﹣3=7cm，而3+3＜7，不满足三角形的三边关系．

    故底边长是：3cm．

    故答案是：3．

    【点评】本题主要考查了等腰三角形的计算，正确理解分两种情况讨论，并且注意到利用三角形的三边关系定理，是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    =0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为(     )

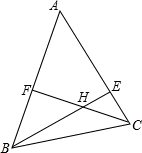
    A．160°  B．150°  C．140°  D．130°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，AB=AC，∠BAC=90°，O为BC的中点．

    （1）写出点O到△ABC的三个顶点A、B、C的距离的关系（不要求证明）

    （2）如果点M、N分别在线段AB、AC上移动，在移动过程中保持AN=BM，请判断△OMN的形状，请证明你的结论．

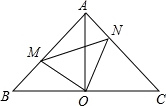
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，∠A，∠B，∠C的对边分别为a、b、c，下列说法中错误的(     )

    A．如果∠C﹣∠B=∠A，则△ABC是直角三角形，且∠C=90°

    B．如果c2=a2﹣b2，则△ABC是直角三角形，且∠C=90°

    C．如果（c+a）（c﹣a）=b2，则△ABC是直角三角形，且∠C=90°

    D．如果∠A：∠B：∠C=3：2：5，则△ABC是直角三角形，且∠C=90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知△ABC中，∠C是其最小的内角，如果过顶点B的一条直线把这个三角形分割成了两个三角形，其中一个为等腰三角形，另一个为直角三角形，则称这条直线为△ABC的关于点B的伴侣分割线．例如：如图1，在Rt△ABC中，∠C=20°，过顶点B的一条直线BD交AC于点D，且∠DBC=20°，显然直线BD是△ABC的关于点B的伴侣分割线．

    （1）如图2，在△ABC中，∠C=20°，∠ABC=110°．请在图中画出△ABC的关于点B的伴侣分割线，并标注角度；

    （2）在△ABC中，设∠B的度数为y，最小内角∠C的度数为x．试探索y与x之间满足怎样的关系时，△ABC存在关于点B的伴侣分割线．

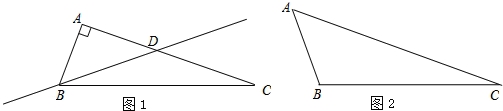
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直角三角形斜边上的高与中线分别是5cm和6cm，则它的面积是__________cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，AD⊥BC于D，要使△ABD≌△ACD，若添加条件∠B=∠C，则可用(     )

    A．SSS  B．AAS  C．HL    D．不确定

    查看答案和解析>>

    同步练习册答案