
△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的( )
A.如果∠C﹣∠B=∠A,则△ABC是直角三角形,且∠C=90°
B.如果c2=a2﹣b2,则△ABC是直角三角形,且∠C=90°
C.如果(c+a)(c﹣a)=b2,则△ABC是直角三角形,且∠C=90°
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90°
B【考点】勾股定理的逆定理.
【分析】根据勾股定理的逆定理以及直角三角形的各种判定方法逐项分析即可.
【解答】解:
A、因为∠C﹣∠B=∠A,∠C+∠B+∠A=180°,所以2∠C=180°,即∠C=90°,故选项正确;
B、因为c2=a2﹣b2,所以如果a2=b2+c2,则△ABC是直角三角形,且∠A=90,不是∠C=90°,故该选项错误;
C 、因为(c+a)(c﹣a)=
、因为(c+a)(c﹣a)= b2,所以C2=a2+b2,则△ABC是直角三角形,且∠C=90°,故选项正确;
b2,所以C2=a2+b2,则△ABC是直角三角形,且∠C=90°,故选项正确;
D、因为 ∠A:∠B:∠C=3:2:5,所以∠A=54°,∠B=36°,∠C=90°,则△ABC是直角三角形,且∠C=90°,故选项正确;
∠A:∠B:∠C=3:2:5,所以∠A=54°,∠B=36°,∠C=90°,则△ABC是直角三角形,且∠C=90°,故选项正确;
故选B.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可,解题的关键是熟记直角三角形的各种判定方法,并能够灵活运用.


科目:初中数学 来源: 题型:
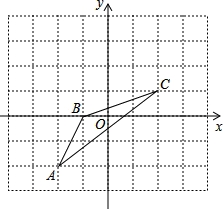
如图:
(1)作出 与△ABC关于x轴对称的图形△A1B1C1;
与△ABC关于x轴对称的图形△A1B1C1;
(2)若图中一个小正方形边长为一个单位长度,请写出各点的坐标:A1__________;B1__________;C1__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
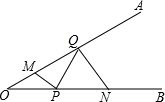
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
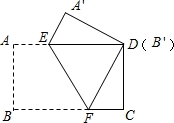
把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求:
(1)DF的长;
(2)重叠部分△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com