Question

把一张长方形纸片按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB=3cm，BC=5cm，求：

（1）DF的长；

（2）重叠部分△DEF的面积．

Answer 1

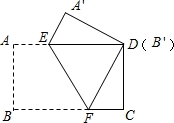
【考点】翻折变换（折叠问题）．

【分析】（1）根据折叠的性质知：BF=DF，用DF表示出FC，在Rt△DCF中，利用勾股定理可求得DF的长；

（2）作FH⊥AD于点H，求得FH，由折叠的性质和平行线的性质证得∠EFD=∠DEF，得出DE=DF，进一步利用三角形的面积计算公式即可求解．

【解答】解：（1）设DF=x，

由折叠可知BF=DF=x，

∴FC=BC﹣BF=5﹣x，

∵四边形ABCD为长方形，

∴DC=AB=3，∠C=90°，AD∥BC，

在Rt△DCF中，∠C=90°，DF²=DC²+FC²

x²=3²+（5﹣x）²

 x=3.4，

∴DF=3.4Ccm；

（2）作FH⊥AD于点H，

则FH=AB=3，

由折叠可知，

∠EFB=∠EFD，

∵AD∥BC，

∴∠DEF=∠EFB，

∴∠EFD=∠DEF，

∴ED=DF=3.4，

S△DEF=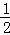×DE×FH=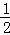×3.4×3=5.1．

【点评】此题主要考查了翻折变换的性质，勾股定理等运用，矩形的性质，三角形的面积，掌握折叠的性质得出对应的线段和角相等是解决问题的关键．