
小强想知道广场上旗杆的高度,他发现旗杆顶端的绳子垂到旗台上还多0.8米,当他把绳子的下端在旗台上拉开2米后,发现下端刚好接触旗台面,你能帮他算出来这根旗杆的高吗?

科目:初中数学 来源: 题型:
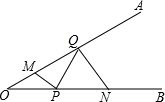
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在第1个△ABA1中,∠B=52°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此作法进行下去,第2014个三角形的底角的度数为( )
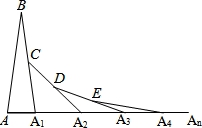
A. B.
B.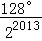 C.
C.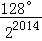 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
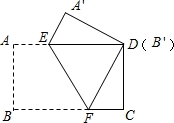
把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求:
(1)DF的长;
(2)重叠部分△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠B=36°,∠C=72°,AD平分∠BAC交BC于点D.下列结论中错误的是( )
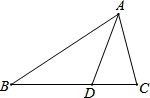
A.图中共有三个等腰三角形 B.点D在AB的垂直平分线上
C.AC+CD=AB D.BD=2CD
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.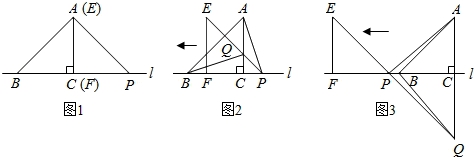
查看答案和解析>>
科目:初中数学 来源: 题型:
请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )
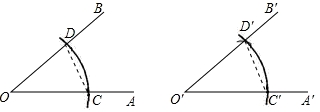
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
将长方形纸片ABCD按如下顺序进行折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);请你求出图②中∠BCB′的度数.
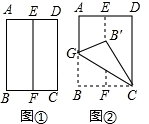
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com