
如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.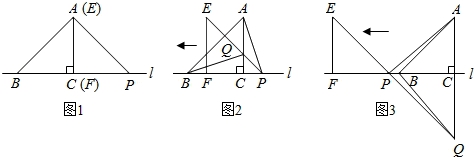
【考点】全等三角形的判定与性质;平移的性质.
【专题】探究型.
【分析】(1)根据图形就可以猜想出结论.
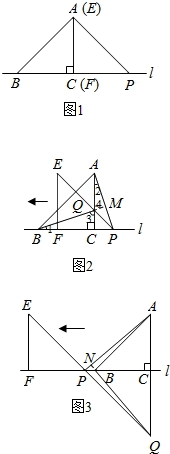
(2)要证BQ=AP,可以转化为证明Rt△BCQ≌Rt△ACP;要证明BQ⊥AP,可以证明∠QMA=90°,只要证出∠1=∠2,∠3=∠4,∠1+∠3=90°即可证出.
(3)类比(2)的证明就可以得到,结论仍成立.
【解答】解:(1)AB=AP;AB⊥AP;
(2)BQ=AP;BQ⊥AP.
证明:①由已知,得EF=FP,EF⊥FP,
∴∠EPF=45°.
又∵AC⊥BC,
∴∠CQP=∠CPQ=45°.
∴CQ=CP.
∵在Rt△BCQ和Rt△ACP中,
BC=AC,∠BCQ=∠ACP=90°,CQ=CP,
∴△BCQ≌△ACP(SAS),
∴BQ=AP.
②如图,延长BQ交AP于点M.
∵Rt△BCQ≌Rt△ACP,
∴∠1=∠2.
∵在Rt△BCQ中,∠1+∠3=90°,又∠3=∠4,
∴∠2+∠4=∠1+∠3=90°.
∴∠QMA=90°.
∴BQ⊥AP;
(3)成立.
证明:①如图,∵∠EPF=45°,
∴∠CPQ=45°.
又∵AC⊥BC,
∴∠CQP=∠CPQ=45°.
∴CQ=CP.
∵在Rt△BCQ和Rt△ACP中,
BC=AC,CQ=CP,∠BCQ=∠ACP=90°,
∴Rt△BCQ≌Rt△ACP.
∴BQ=AP.
②如图③,延长QB交AP于点N,则∠PBN=∠CBQ.
∵Rt△BCQ≌Rt△ACP,
∴∠BQ C=∠APC.
C=∠APC.
∵在Rt△BCQ中,∠BQC+∠CBQ=90°,
又∵∠CBQ=∠PBN,
∴∠APC+∠PBN=90°.
∴∠PNB=90°.
∴QB⊥AP.
【点评】证明两个线段相等可以转化为证明三角形全等的问题.证明垂直的问题可以转化为证明两直线所形成的角是直角来解决.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
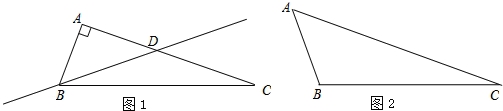
已知△ABC中,∠C是其最小的内角,如果过顶点B的一条直线把这个三角形分割成了两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC的关于点B的伴侣分割线.例如:如图1,在Rt△ABC中,∠C=20°,过顶点B的一条直线BD交AC于点D,且∠DBC=20°,显然直线BD是△ABC的关于点B的伴侣分割线.
(1)如图2,在△ABC中,∠C=20°,∠ABC=110°.请在图中画出△ABC的关于点B的伴侣分割线,并标注角度;
(2)在△ABC中,设∠B的度数为y,最小内角∠C的度数为x.试探索y与x之间满足怎样的关系时,△ABC存在关于点B的伴侣分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
小强想知道广场上旗杆的高度,他发现旗杆顶端的绳子垂到旗台上还多0.8米,当他把绳子的下端在旗台上拉开2米后,发现下端刚好接触旗台面,你能帮他算出来这根旗杆的高吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 ,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为__________.
,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com