
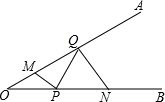
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是__________.
 .
.
【考点】轴对称-最短路线问题.
【专题】压轴题.
【分析】作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.
【解答】解:作M关于OB的对称点M′,作N关于OA的对称点N′,
连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,
∴在Rt△M′ON′中,
M′N′= =
= .
.
故答案为 .
.

【点评】本题考查了轴对称﹣﹣最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.

查看答案和解析>>
科目:初中数学 来源: 题型:
△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的( )
A.如果∠C﹣∠B=∠A,则△ABC是直角三角形,且∠C=90°
B.如果c2=a2﹣b2,则△ABC是直角三角形,且∠C=90°
C.如果(c+a)(c﹣a)=b2,则△ABC是直角三角形,且∠C=90°
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
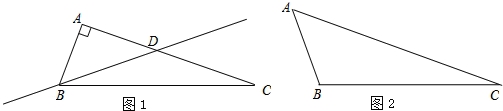
已知△ABC中,∠C是其最小的内角,如果过顶点B的一条直线把这个三角形分割成了两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为△ABC的关于点B的伴侣分割线.例如:如图1,在Rt△ABC中,∠C=20°,过顶点B的一条直线BD交AC于点D,且∠DBC=20°,显然直线BD是△ABC的关于点B的伴侣分割线.
(1)如图2,在△ABC中,∠C=20°,∠ABC=110°.请在图中画出△ABC的关于点B的伴侣分割线,并标注角度;
(2)在△ABC中,设∠B的度数为y,最小内角∠C的度数为x.试探索y与x之间满足怎样的关系时,△ABC存在关于点B的伴侣分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )

A.垂直 B.相等 C.平分 D.平分且垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
小强想知道广场上旗杆的高度,他发现旗杆顶端的绳子垂到旗台上还多0.8米,当他把绳子的下端在旗台上拉开2米后,发现下端刚好接触旗台面,你能帮他算出来这根旗杆的高吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com