练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，A、B两点分别在x轴和y轴上，OA=1，OB= ，连接AB，过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1 ， 连接A1B1 ， 再过A1B1中点C2作x轴和y轴的垂线，照此规律依次作下去，则点Cn的坐标为 ．

    【答案】
    【解析】解：∵过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1 ，
    ∴B1C1和C1A1是三角形OAB的中位线，
    ∴B1C1= OA= ，C1A1= OB= ，
    ∴C1的坐标为（ ， ），
    同理可求出B2C2= = ，C2A2= =
    ∴C2的坐标为（ ， ），
    …以此类推，
    可求出BnCn= ，CnAn= ，
    ∴点Cn的坐标为 ，
    故答案为： ．
    首先利用三角形中位线定理可求出B1C1的长和C1A1的长，即C1的横坐标和纵坐标，以此类推即可求出点Cn的坐标．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

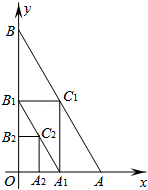
    科目：初中数学 来源： 题型：

    【题目】我们知道：任意一个有理数与无理数的和为无理数，任意一个不为零的有理数与一个无理数的积为无理数，而零与无理数的积为零．由此可得：如果ax+b=0，其中a、b为有理数，x为无理数，那么a=0且b=0．

    运用上述知识，解决下列问题：

    （1）如果（a-2）+b+3=0，其中a、b为有理数，那么a= ，b= ；

    （2）如果（2+）a-（1-）b=5，其中a、b为有理数，求a+2b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．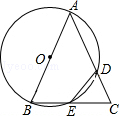
    （1）求证：AB=AC；
    （2）若AB=4，BC=2 ，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某次篮球联赛初赛阶段，每队有场比赛，每场比赛都要分出胜负，每队胜一场得分， 负一场得分，积分超过分才能获得参赛资格.

    （1）已知甲队在初赛阶段的积分为分，求甲队初赛阶段胜、负各多少场；

    （2）如果乙队要获得参加决赛资格，那么乙队在初赛阶段至少要胜多少场？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC，点D、F分别为线段AC、AB上两点，连接BD、CF交于点E．

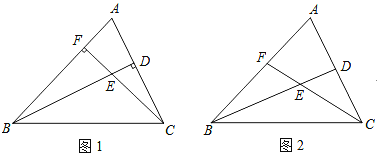
    （1）若BD⊥AC，CF⊥AB，若BE=4，CE=2，求CD：BF；

    （2）若BD平分∠ABC，CF平分∠ACB，如图2所示，猜想∠BEC与∠A的数量关系；并说明理由．

    （3）在（2）的条件下，若∠A=60°，试说明：BC=BF+CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD于F．

    （1）求证：△AEF≌△BEC；

    （2）判断四边形BCFD是何特殊四边形，并说出理由；

    （3）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，若BC=1，求AH的长．

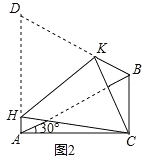
    查看答案和解析>>

    科目：初中数学 来源： 题型：

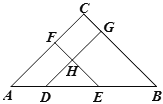
    【题目】如图，在△ABC中 ，∠A=∠B，D、E是边AB上的点，DG∥AC，EF∥BC，DG、EF相 交于点H．

    (1)∠HDE与∠HED是否相等？并说明理由．

    解:∠HDE=∠HED．理由如下：

    ∵DG∥AC(已知)

    ∴　 　　＝　 　　 （ 　　 　　 　　）

    ∵ EF∥BC (已知)

    ∴　　 　＝　 　　 （ 　 　）

    又∵∠A=∠B (已知)

    ∴ ＝ （ ）.

    (2)如果∠C=90°，DG、 EF有何位置关系？并仿照 (1)中的解答方法说明理由．

    解：　　　　　　　　．理由如下：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果m是从﹣1，0，1，2四个数中任取的一个数，n是从﹣2，0，3三个数中任取的一个数，则二次函数y=（x﹣m）2+n的顶点在坐标轴上的概率为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（ ）﹣1+（3﹣π）°﹣|1﹣tan60°|+ ÷2．

    查看答案和解析>>

    同步练习册答案