
【题目】已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
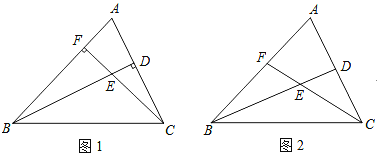
(1)若BD⊥AC,CF⊥AB,若BE=4,CE=2,求CD:BF;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,猜想∠BEC与∠A的数量关系;并说明理由.
(3)在(2)的条件下,若∠A=60°,试说明:BC=BF+CD.
【答案】(1)1:2(2)∠BEC=90°+![]() ∠A(3)证明见解析
∠A(3)证明见解析
【解析】
(1)根据∠BEF=∠CED,∠BFE=∠CDE=90°可证明△BEF∽△CED,根据相似三角形的性质即可得答案;(2)根据角平分线的性质得到∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,根据三角形内角和定理即可得到结论;(3)在BC上截取BM=BF,连接EM,根据SAS可证明△BEF≌△BEM,可得∠BEF=∠BEM,由(2)可得∠BEC=120°,即可证∠∠BEF=∠BEM=∠CEM=∠CED=60°,即可证明△CEM≌△CED,进而可得CD=CM,即可证明BC=BF+CD.
∠ACB,根据三角形内角和定理即可得到结论;(3)在BC上截取BM=BF,连接EM,根据SAS可证明△BEF≌△BEM,可得∠BEF=∠BEM,由(2)可得∠BEC=120°,即可证∠∠BEF=∠BEM=∠CEM=∠CED=60°,即可证明△CEM≌△CED,进而可得CD=CM,即可证明BC=BF+CD.
(1)∵∠BEF=∠CED,∠BFE=∠CDE=90°,
∴△BEF∽△CED,
∴![]()
∵BE=4,CE=2,
∴CD:BF=1:2.
(2)∠BEC =90°+![]() ∠A;理由如下:
∠A;理由如下:
∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠BEC=180°-![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴∠BEC=180°-![]() (180°-∠A)=90°+∠A.
(180°-∠A)=90°+∠A.
(3)如图:在BC上截取BM=BF,连接EM,
∵∠A=60°,
∴由(2)可知∠BEC=90°+![]() ∠A=120°,
∠A=120°,
∴∠BEF=60°,
∵BE平分∠ABC,
∴∠FBE=∠EBM,
∵BF=BM,∠FBE=∠EBM,BE=BE,
∴△BEF≌△BEM(SAS),
∴∠BEM=∠BEF=60°,
∴∠CEM=60°,
∴∠CED=∠CEN=60°,
∵CE平分∠ACB,
∴∠DCE=∠MCE,
∵∠CED=∠CEN=60°,CE=CE,∠DCE=∠MCE,
∴△CEM≌△CED(ASA),
∴CD=CM,
∴BC=BM+CM=BF+CD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点. 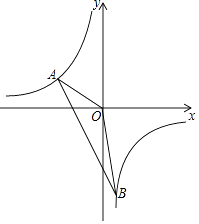
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
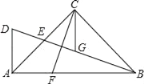
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上﹣点,连接CF,且∠ACF=∠CBG.
(1)求证:AF=CG;
(2)写出图中长度等于2DE的所有线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
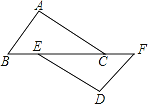
【题目】如图,已知点B、E、C、F在一条直线上,AC∥DE,AC=DE,∠A=∠D.
(1)求证:AB=DF;
(2)若BC=9,EC=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB= ![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1 , 连接A1B1 , 再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 . 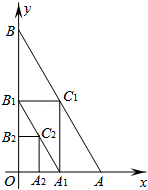
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)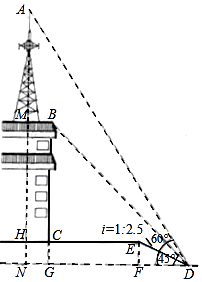
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有22名工人,每人每天可生产1200个螺钉或2000个螺母,1个螺钉需配2个螺母,为使生产的螺钉和螺母刚好配套,若设x名工人生产螺钉,依题意列方程为( )
A. 1200x=2000(22-x) B. 1200x=2![]() 2000(22-x)
2000(22-x)
C. 1200(22-x)=2000x D. 2![]() 1200x=2000(22-x)
1200x=2000(22-x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com