
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.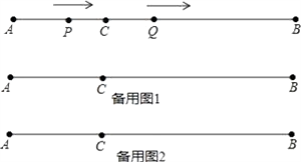
(1)AC=cm,BC=cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.
【答案】
(1)4;8
(2)解:由题意可知:AP=3t,PQ=4﹣(3t﹣t),
则3t=4﹣(3t﹣t),
解得:t= ![]() .
.
答:当t= ![]() 时,AP=PQ
时,AP=PQ
(3)解:∵点P、Q相距的路程为1cm,
∴(4+t)﹣3t=1(相遇前)或3t﹣(4+t)=1(第一次相遇后),
解得t= ![]() 或t=
或t= ![]() ,
,
当到达B点时,第一次相遇后点P、Q相距的路程为1cm,
3t+4+t=12+12﹣1
解得:t= ![]() .
.
答:当t为 ![]() ,
, ![]() ,
, ![]() 时,PQ=1cm
时,PQ=1cm
【解析】(1)∵AB=12cm,点C是线段AB上的一点,BC=2AC,
∴AC+BC=3AC=AB=12cm,
∴AC=4cm,BC=8cm;
(1)根据AB=12cm,点C是线段AB上的一点,BC=2AC,得出AB=AC+BC=3AC=12cm ,进而得出答案AC=4cm,BC=8cm ;
(2)由题意可知:AP=3t,PQ=4﹣(3t﹣t),然后由AP=PQ;列出关于t的方程,求解得出t的值 ;
(3)此题分三种情况:①相遇前,由PQ=1列出方程(4+t)﹣3t=1 ;②第一次相遇后由PQ=1列出方程3t﹣(4+t)=1 ,③当到达B点时,第一次相遇后点P、Q相距的路程为1cm,列出方程3t+4+t=12+12﹣1 ,分别解方程求出t的值即可 。


科目:初中数学 来源: 题型:
【题目】胡老师计划组织朋友暑假去革命圣地延安两日游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费,假设组团参加甲、乙两家旅行社两日游的人数均为x人.
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你计算,在甲、乙两家旅行社中,帮助胡老师选择收取总费用较少的一家.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要了解全校学生课外作业负担情况,你认为以下抽样方式比较合理的是( )
A. 调查全体男学生 B. 调查全体女学生
C. 调查七年级全体学生 D. 调查各年级中的部分学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行书法比赛,为奖励优胜学生,购买了一些钢笔和毛笔,毛笔单价是钢笔单价的1.5倍,购买钢笔用了1500元,购买毛笔用了1800元,购买的钢笔支数比毛笔多30支,钢笔、毛笔的单价分别是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com