
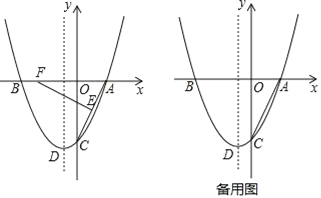
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于点A(2,0)和点B,与y轴交于点C,顶点为点D,对称轴为直线x=﹣1,点E为线段AC的中点,点F为x轴上一动点.
(1)直接写出点B的坐标,并求出抛物线的函数关系式;
(2)当点F的横坐标为﹣3时,线段EF上存在点H,使△CDH的周长最小,请求出点H,使△CDH的周长最小,请求出点H的坐标;
(3)在y轴左侧的抛物线上是否存在点P,使以P,F,C,D为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)B(﹣4,0),y=![]() x2+x﹣4;(2)H(
x2+x﹣4;(2)H(![]() ,
, ![]() );(3)存在,点P的坐标为(﹣1﹣2
);(3)存在,点P的坐标为(﹣1﹣2![]() ,﹣
,﹣![]() ),(﹣1﹣
),(﹣1﹣![]() ,
, ![]() ).
).
【解析】试题分析:(1)根据轴对称,可得B点坐标,根据待定系数法,可得答案;
(2)根据自变量与函数值的对应关系,可得C点坐标,根据配方法,可得D点坐标,根据勾股定理,可得CF的长,根据等腰三角形的性质,可得A,C关于EF对称,根据轴对称的性质,可得PA=PC,根据两点之间线段最短,可得P是AD与EF的交点,根据解方程组,可得答案;
(3)根据平行四边形的对角线互相平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得答案.
解:(1)由A、B关于x=﹣1对称,得
B(﹣4,0),
∵抛物线y=ax2+bx﹣4过A(2,0)、B(﹣4,0),
∴![]() ,
,
解得: 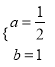 ,
,
∴y=![]() x2+x﹣4,
x2+x﹣4,
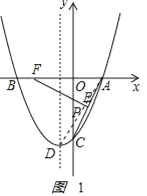
(2)如图1
 ,
,
当x=0时,y=﹣4,即C(0,﹣4),
y=![]() x2+x﹣4=
x2+x﹣4=![]() (x+1)2﹣
(x+1)2﹣![]()
∴D(﹣1,﹣ ![]() ),
),
∵E为线段AC的中点,A(2,0),C(0,﹣4),
∴E(1,﹣2).
∵点F横坐标为﹣3,
∴F(﹣3,0),
∴AF=5,CF=![]() =
=![]() =5,
=5,
∴AF=CF,
∵E为线段AC的中点,
∴EF垂直平分AC,
∴A、C关于直线EF轴对称,连接AD,与直线EF交点即为所求H,
∴EF⊥AC.
设直线EF关系式为y=k1x+b1,
∴![]() ,
,
解得: 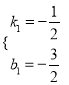 ,
,
∴直线EF:y=﹣![]() x﹣
x﹣![]() ,
,
设直线AD关系式为y=k2x+b2,
∴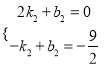 ,
,
解得: 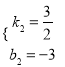 ,
,
∴y=![]() x﹣3,
x﹣3,
联立AD,EF,得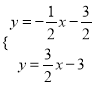 ,
,
∴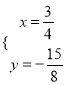 ,
,
∴H(![]() ,
, ![]() ).
).
(3)若CD为对角线,不存在;
若CD为边,则PF∥CD且PF=CD,
∵C(0,﹣4),D(﹣1,﹣ ![]() ),点F为x轴上一动点,
),点F为x轴上一动点,
如图2
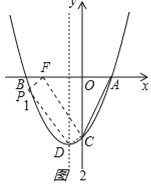 ,
,
PDCF是平行四边形,对角线的纵坐标为﹣![]() ,P点纵坐标﹣
,P点纵坐标﹣![]() ,
,
当y=﹣![]() 时,
时, ![]() x2+x﹣4=﹣
x2+x﹣4=﹣![]() ,解得x1=﹣1+2
,解得x1=﹣1+2![]() (舍),x2=﹣1﹣2
(舍),x2=﹣1﹣2![]() ,
,
∴P1(﹣1﹣2![]() ,﹣
,﹣![]() ).
).
如图3
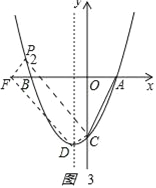 ,
,
PFDC是平行四边形,对角线的交点坐标为﹣2,P点坐标为![]() ,
,
当y=![]() 时,
时, ![]() x2+x﹣4=
x2+x﹣4=![]() ,解得x1=﹣1+
,解得x1=﹣1+![]() (舍),x2=﹣1﹣
(舍),x2=﹣1﹣![]() ,
,
∴P2(﹣1﹣![]() ,
, ![]() ).
).
综上所述:在y轴左侧的抛物线上存在点P,使以P,F,C,D为顶点的四边形是平行四边形,点P的坐标(﹣1﹣2![]() ,﹣
,﹣![]() ),(﹣1﹣
),(﹣1﹣![]() ,
, ![]() ).
).


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】一次模拟考试后,数学陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的百分比之和是14%;②第一组的百分比是2%;③自左到右第二、三、四组的频数比为3∶9∶8,然后布置学生(也请你一起)结合统计图完成下列问题:
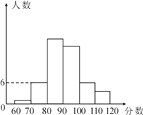
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次射击训练中,甲、乙两人各射击10次,两人10次射击成绩的平均数均是9.1环,方差分别是S甲2=1.2,S乙2=1.6,则关于甲、乙两人在这次射击训练中成绩稳定的描述正确的是( )
A. 甲比乙稳定 B. 乙比甲稳定
C. 甲和乙一样稳定 D. 甲、乙稳定性没法对比
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有13位同学参加学校组织的才艺表演比赛.已知他们所得的分数互不相同,共设7个获奖名额.某同学知道自己的比赛分数后,要判断自己能否获奖,在下列13名同学成绩的统计量中只需知道一个量,它是( )
A. 众数 B. 方差 C. 中位数 D. 平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③
B.②③
C.③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=![]() AB中,一定正确的是( )
AB中,一定正确的是( )
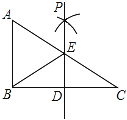
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com