已知关于x的一元二次方程2x2﹣3mx﹣5=0的一个根是﹣1，则m=
阅读快车系列答案科目：初中数学 来源： 题型：
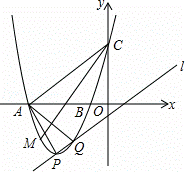
已知抛物线y=x2﹣2mx+m2+m﹣1（m是常数）的顶点为P，直线l：y=x﹣1
（1）求证：点P在直线l上；
（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；
（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列四个命题中，正确的是 （填写正确命题的序号）
①三角形的外心是三角形三边垂直平分线的交点；
②函数y=（1﹣a）x2﹣4x+6与x轴只有一个交点，则a=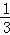
；
③半径分别为1和2的
两圆相切，则两圆的圆心距为3；
④若对于任意x＞1的实数，都有ax＞1成立，则a的取值范围是a≥1．
查看答案和解析>>
科目：初中数学 来源： 题型：
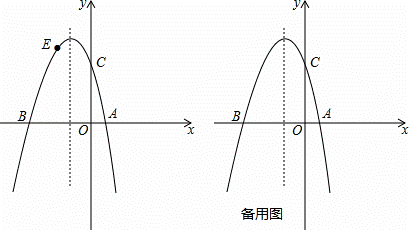
如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．
（1）求此抛物线的解析式；
（2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；
（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
北京在今年6月初申办2022年冬季奥运会的陈述中，若申办成功，将带动月3.2亿人参与这项活动．将3.2亿用科学记数法表示为（ ）
A． 32×107 B． 3.2×108 C． 3.2×109 D． 0.32×1010
查看答案和解析>>
科目：初中数学 来源： 题型：
我国是世界上严重缺失的国家之一，全国总用水量逐年上升，全国总用水量可分为农业用水量、工业用水量和生活用水量三部分．为了合理利用水资
源，我国连续多年对水资源的利用情况进行跟踪调查，将所得数据进行处理，绘制了2008年全国总用水量分布情况扇形统计图和2004﹣2008年全国生活用水量折线统计图的一部分如下：
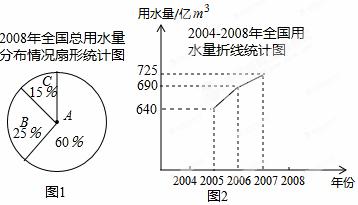
（1）2007年全国生活用水量比2004年增加了16%，则2004年全国生活用水量为 亿m3，2008年全国生活用水量比2004年增加了20%，则2008年全国生活用水量为 
亿m3；
（2）根据以上信息，
请直接在答题卡上补全折线统计图；
（3）根据以上信息2008年全国总水量为 亿；
（4）我国2008年水资源总量约为2.75×104亿m3，根据国外的经验，一个国家当年的全国总用水量超过这个国家年水资源总量的20%，就有可能发生“水危机”．依据这个标准，2008年我国是否属于可能发生“水危机”的行列？并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，解得a=
，解得m=1．
的根是____________．
等于（ ）
B． 
C． 
D． 