
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
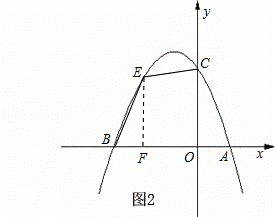
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
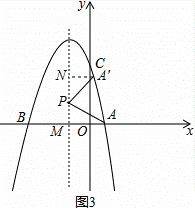
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
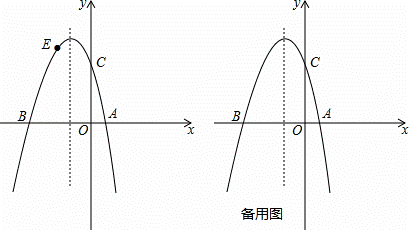
解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴c=3,
∴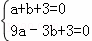 ,
,
解得: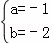 ,
,
∴所求抛物线解析式为:y=﹣x2﹣2x+3;
(2)如图2,过点E作EF⊥x轴于点F,设E(a,﹣a2﹣2a+3)(﹣3<a<0)
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴S四边形BOCE=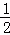 BF•EF+
BF•EF+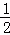 (OC+EF)•OF,
(OC+EF)•OF,
=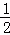 (a+3)•(﹣a2﹣2a+3)+
(a+3)•(﹣a2﹣2a+3)+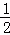 (﹣a2﹣2a+6)•(﹣a),
(﹣a2﹣2a+6)•(﹣a),
=﹣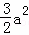 ﹣
﹣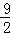 a+
a+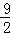 ,
,
=﹣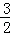 (a+
(a+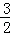 )2+
)2+ ,
,
∴当a=﹣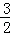 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为 .
.
此时,点E坐标为(﹣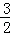 ,
,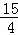 );
);
(3)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,点P在抛物线的对称轴上,
∴设P(﹣1,m),
∵线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,如图,
∴PA=PA′,∠APA′=90°,
如图3,过A′作A′N⊥对称轴于N,设对称轴于x轴交于点M,
∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°,
∴∠NA′P=∠NPA,
在△A′NP与△APM中,
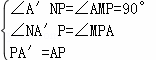 ,
,
∴△A′NP≌△PMA,
∴A′N=PM=|m|,PN=AM=2,
∴A′(m﹣1,m+2),
代入y=﹣x2﹣2x+3得:m +2=﹣(m﹣1)2﹣2(m﹣1)+3,
+2=﹣(m﹣1)2﹣2(m﹣1)+3,
解得:m=1,m=﹣2,
∴P(﹣1,1),(﹣1,﹣2).


科目:初中数学 来源: 题型:
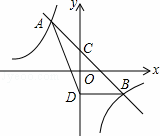
如图,直线y=mx+n与双曲线y= 相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABM=2∠BAM.
(1)求证:AG=BG;
(2)若点M为BC的中点,同时S△BMG=1,求三角形ADG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
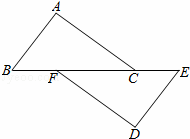
如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 (只需写一个,不添加辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
为了解全校学生上学的交通方式,该校九年级(8)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,并把条形统计图补充完整;
(2)在扇形统计图中,“步行”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com