练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

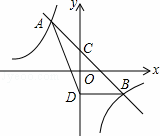
    如图，直线y=mx+n与双曲线y=相交于A（﹣1，2），B（2，b）两点，与y轴相交于点C．

    （1）求m，n的值；

    （2）若点D与点C关于x轴对称，求△ABD的面积．


    解：（1）把x=﹣1，y=2；x=2，y=b代入y=，

    解得：k=﹣2，b=﹣1；

    把x=﹣1，y=2；x=2，y=﹣1代入y=mx+n，

    解得：m=﹣1，n=1；

    （2）直线y=﹣x+1与y轴交点C的坐标为（0，1），所以点D的坐标为（0，﹣1），

    点B的坐标为（2，﹣1），所以△ABD的面积=．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，一次函数y1=x+b与一次函数y2=kx+4的图象交于点P（1，3），则关于x的不等式x+b＞kx+4的解集是（　　）

     

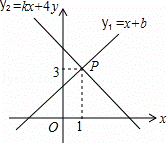
    　    A． x＞﹣2    B． x＞0       C． x＞1       D． x＜1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


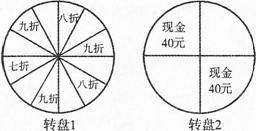
    某商场举行开业酬宾活动，设立了两个可以自由转动的转盘（如图所示，两个转盘均被等分）．并规定：顾客购买满188元的商品，即可任选一个转盘转动一次，转盘停止后，指针所指区域内容即为优惠方式；若指针所指区域空白，则无优惠．已知小张在该商场消费300元．

    (1)若他选择转动转盘1，则他能得到优惠的概率为多少？

    (2)选择转动转盘1和转盘2，哪种方式对于小张更合算，请通过计算加以说明．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知方程2x2+4x﹣3=0的两根分别为x1和x2，则x1+x2的值等于　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：（﹣2）2﹣+（﹣3）0﹣（）﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


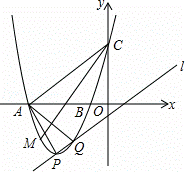
    已知抛物线y=x2﹣2mx+m2+m﹣1（m是常数）的顶点为P，直线l：y=x﹣1

    （1）求证：点P在直线l上；

    （2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；

    （3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某商品的外包装盒的三视图如图所示，则这个包装盒的体积是（　　）

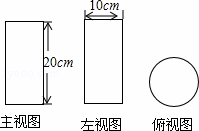
    　   A．200πcm3          B． 500πcm3                C．                             1000πcm3 D． 2000πcm3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


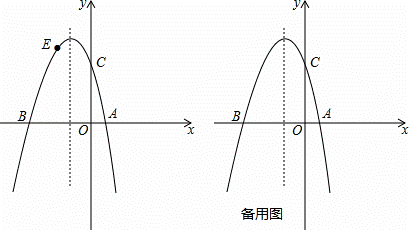
    如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．

    （1）求此抛物线的解析式；

    （2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；

    （3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简﹣的结果为（　　）

    　   A．              B．                    C．                       D．

    查看答案和解析>>

    同步练习册答案