
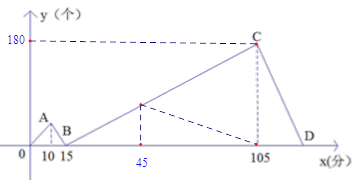
【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量![]() (个)与加工时间
(个)与加工时间![]() (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

【答案】(1)B(15,0),甲乙两人工作15分钟时,加工零件的数量相同
(2)y=2x-30,D(150,0)(3)65分钟或125分钟(4)第45分钟
【解析】试题分析:(1)观察图象即可得出点B的坐标,然后根据纵坐标的意义可知此时两人加工的零件数量相同;
(2)利用待定系数法即可得BC对应的函数关系式,根据图象可知105分钟时甲完成任务,甲实际用了100分钟完成任务,从而得到甲的速度,继而知道乙的速度,从而得出点D坐标;
(3)求出CD段的解析式,分别所y=100代入BC、CD段解析式即可得;
(4)设丙应该在x分钟时加入,根据等量关系:乙x分钟加工的数量+乙、丙(105-x)分钟加工的数量=600,解方程即可得,然后补全图象即可.
试题解析:(1)由图象可知B(15,0),根据纵轴表示甲比乙多加工的零件数量可知此时甲、乙加工的零件数量相同,
故答案为:(15,0),甲乙两人工作15分钟时,加工零件的数量相同;
(2)设直线BC的解析式为:y=kx+b,由题意则有
![]() ,解得:
,解得: ![]() ,所以BC段的函数关系式为:y=2x-30,
,所以BC段的函数关系式为:y=2x-30,
由图象可知105分钟时甲完成了任务,甲中间休息了5分钟,105-5=100,
600÷100=6,6-2=4,600÷4=150,所以D(150,0);
(3)把y=100代入y=2x-30,得:100=2x-30,解得:x=65,
设直线CD的解析式为:y=ax+e,由题意则有
![]() ,解得:
,解得: ![]() ,所以BC的函数关系式为:y=-4x+600,
,所以BC的函数关系式为:y=-4x+600,
当y=100时,有100=-4x+600,解得:x=125,
所以乙在加工的过程中,65或125分钟时比甲少加工100个零件;
(4)设x分钟时丙加入,则有:4x+(4+3)(105-x)=600,解得:x=45,
即:丙在45分钟时开始帮助乙,
图象如图所示:


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
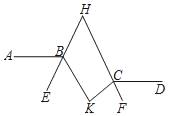
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.



(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)著点P在图(2)位置时,请写出∠1、∠2、∠3之间的关系,并说明理由;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,入射角∠ODE与反射角∠ADC相等,则∠DEB的度数是( )

A. 75°36′ B. 75°12′ C. 74°36′ D. 74°12′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,点C(1,n)在直线AB上,点D在y轴的负半轴上,且CD=![]() .
.
(1)求点C、点D的坐标.
(2)若P为y轴上的点,当△PCD为等腰三角形时,求点P的坐标.
(3)若点M为x轴上一动点(点M不与点O重合),N为直线y=2x-5上一动点,是否存在点M、N,使得△AMN与△AOB全等?若存在,求出点N的坐标;若不存在,请说明理由.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
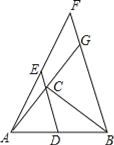
【题目】如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=![]() CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AB=BG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
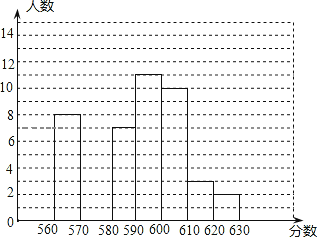
【题目】已知小红的成绩如下表:
文化成绩 | 综合素 质成绩 | 总成绩 | |||
测验1 | 测验2 | 测验3 | |||
小红 | 560分 | 580分 | 630分 | 12 | |
(1)小红的这三次文化测试成绩的平均分是_____分;
(2)用(1)中的平均分加上综合素质成绩就是小红的总成绩.用同样的方法计算出小红所在班级全部同学的总成绩并绘制出了如图所示的频数分布直方图.那么小红所在班级共有_____名同学;
(3)学校将根据总成绩由高到低保送小红所在班级前15名同学进入高中学习,请问小红能被保送吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com