
 已知圆锥的底面半径为r=20cm,高h=20
已知圆锥的底面半径为r=20cm,高h=20| 15 |
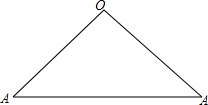 解:(1)∵母线长l=
解:(1)∵母线长l=| r2+h2 |
202+(20
|
| nπ×80 |
| 180 |
| 802+802 |
| 2 |


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
 甲、乙二人乘船从小岛A同时出发,甲的速度为40n mile/h,向北偏东20°的方向航行,乙的速度为30n mile/h,沿南偏东70°的方向航行,
甲、乙二人乘船从小岛A同时出发,甲的速度为40n mile/h,向北偏东20°的方向航行,乙的速度为30n mile/h,沿南偏东70°的方向航行,| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com