
����Ŀ��(1)����
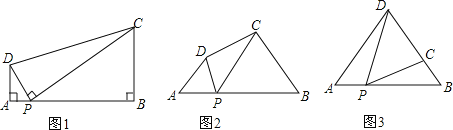
��ͼ1�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=90������֤��ADBC=APBP.
(2)̽��
��ͼ2�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=��ʱ�����������Ƿ���Ȼ������˵������.
(3)Ӧ��
������(1)(2)��õľ��������⣺��ͼ3������ABD�У�AB=6��AD=BD=5����P��ÿ��1����λ���ȵ��ٶȣ��ɵ�A�������ر�AB���B�˶�����������DPC=��A�����P���˶�ʱ��Ϊt(��)������DΪԲ�ģ���DCΪ�뾶��Բ��AB����ʱ����t��ֵ.
���𰸡�(1)֤����������(2)����ADBC=APBP�Գ��������ɼ�������(3)t��ֵΪ2���10�룮
��������
��1������ͬ�ǵ������ȣ�����֤����APD=��BPC��Ȼ��������������ε��ж�����֤������ADP�ס�BPC���ٸ������������ε����ʣ��г�����ʽ�������ݱ����Ļ������ʼ���֤�����ۣ�
��2��������������ǵ����ʺ���֪����֤������BPC=��APD��Ȼ��������������ε��ж�����֤������ADP�ס�BPC���ٸ������������ε����ʣ��г�����ʽ�������ݱ����Ļ������ʼ���֤�����ۣ�
��3������D��DE��AB�ڵ�E���������ߺ�һ���ɶ������DE��Ȼ��Բ�������ߵ����ʿɵã�DC=DE=8���ٸ���(1)(2)�ľ����ADBC=APBP���г����̣����t��ֵ����.
(1)֤�����ߡ�DPC=��A=��B=90�㣬
���ADP+��APD=90�㣬��BPC+��APD=90�㣬
���APD=��BPC��
���ADP�ס�BPC��
��![]()
��ADBC=APBP��
(2)����ADBC=APBP�Գ��������ɣ�
֤�����ߡ�BPD=��DPC+��BPC����BPD=��A+��APD��
���DPC+��BPC=��A+��APD��
�ߡ�DPC=��A=�ȣ�
���BPC=��APD��
�֡ߡ�A=��B=�ȣ�
���ADP�ס�BPC��
��![]() ��
��
��ADBC=APBP��
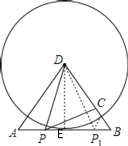
(3)�⣺����ͼ������D��DE��AB�ڵ�E��
��AD=BD=10��AB=12��
��AE=BE=6
���ݹ��ɶ����ɵã�DE=![]() =8��
=8��
����DΪԲ�ģ���DCΪ�뾶��Բ��AB���У�
��DC=DE=8��
��BC=10-8=2��
��AD=BD��
���A=��B��
�֡ߡ�DPC=��A��
���DPC=��A=��B����(1)(2)�ľ����ADBC=APBP��
�֡�AP=t��BP=12-t��
��t(12-t)=10��2��
��t=2��t=10��
��t��ֵΪ2���10�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������M��y��ax2+bx+c��a��0������A����1��0�����Ҷ�������ΪB��0��1����
��1����������M�ĺ�������ʽ��
��2����F��t��0��Ϊx����������һ�㣬��������M�Ƶ�F��ת180��õ�������M1��
��������M1�Ķ���B1������Ϊ�� ����
����������M1���߶�AB�й�����ʱ����Ϻ�����ͼ����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʡʮ���У���24�⣬10�֣���֪OΪֱ��MN��һ�㣬OP��MN���ڵ���Rt��ABO�У���BAO=90�㣬AC��OP��OM��C��DΪOB���е㣬DE��DC��MN��E��
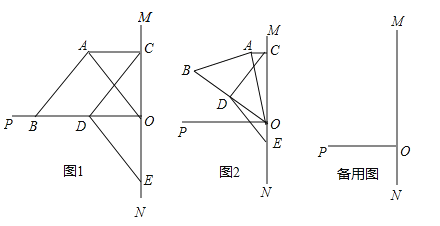
��1����ͼ1������B��OP�ϣ���
��AC OE�����������=����������
���߶�CA��CO��CD����ĵ�����ϵʽ�� ��
��2����ͼ1�еĵ���Rt��ABO��O��˳ʱ����ת����0�㣼����45�㣩����ͼ2����ô��1���еĽ��ۢ��Ƿ��������˵�����ɣ�
��3����ͼ1�еĵ���Rt��ABO��O��˳ʱ����ת����45�㣼����90�㣩��������ͼ3�л���ͼ�Σ���ֱ��д���߶�CA��CO��CD����ĵ�����ϵʽ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x�ύ��A����3��0����B��1��0�����㣬��y���ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��
��1����ֱ��д��D������꣮
��2������κ����Ľ���ʽ��
��3������ͼ��ֱ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij��������������������һ���齱���������ǣ�ֻ�н����������ļס��ҡ�����λͬѧ��ÿ�˲��ܻ��һ�γ齱����������ͼ��ʾ�ķ����������4��������ѡһ�����֣�ѡ�к�Ϳ��Եõ������ֺ������Ӧ��Ʒ��ǰ�����ѡ�е����֣�������˾Ͳ�����ѡ����������
��1��������״ͼ�����б����ķ�����ס��Ҷ��˵õ��Ľ�Ʒ���Ǽ������ĸ�����
��2���е�ͬѧ��Ϊ��������ȷ����ƣ���ô���õ�����ĸ��ʻ��Щ������˵����ȷ����˵��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ��Ѿ�����AC�۵�����B���ڵ�E����AE��DC�Ľ���ΪO������DE��
��1����֤����ADE�ա�CED��
��2����֤��DE��AC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݣ�����Ҫ�������⣺ ���⣺����ƽ���ڣ���֪�ֱ���![]() ���㣬
���㣬![]() ���㣬
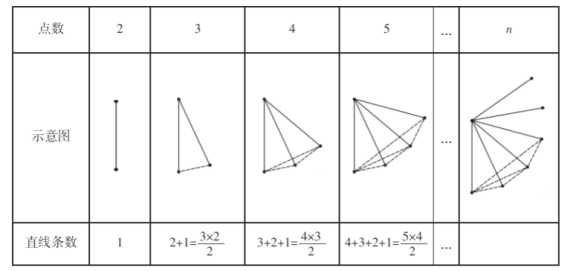
���㣬![]() ���㣬5 ���㣬����n ���㣬���������� ���㶼����ͬһ��ֱ����.����ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ� �� ̽����Ϊ�˽��������⣬ϣ��С���ͬѧ����������±������̽������Ϊ�˷����� �����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
���㣬5 ���㣬����n ���㣬���������� ���㶼����ͬһ��ֱ����.����ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ� �� ̽����Ϊ�˽��������⣬ϣ��С���ͬѧ����������±������̽������Ϊ�˷����� �����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
�����������⣺
��1�������ϣ��С����ɣ���ֱ��д�����ۣ���ƽ������![]() ����ʱ��ֱ������Ϊ ��
����ʱ��ֱ������Ϊ ��
��2����ijͬѧ���ձ����еķ�����������![]() ��ֱ�ߣ����ƽ�����ж��ٸ���֪��.
��ֱ�ߣ����ƽ�����ж��ٸ���֪��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
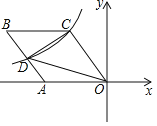
����Ŀ����ͼ������OABC��һ��OA��x��ĸ������ϣ�O������ԭ�㣬tan��AOC=![]() ������������y=
������������y=![]() ��ͼ����C����AB���ڵ�D������COD�����Ϊ20����k��ֵ����_____��
��ͼ����C����AB���ڵ�D������COD�����Ϊ20����k��ֵ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
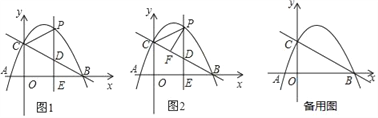
����Ŀ����ͼ1��������y=ax2+bx+c��a��0����x�ύ�ڵ�A����1��0����B��4��0�����㣬��y�ύ�ڵ�C����OC=3OA����P���������ϵ�һ�����㣬����P��PE��x���ڵ�E����ֱ��BC�ڵ�D������PC��
��1���������ߵĽ���ʽ��
��2����ͼ2��������Pֻ�ڵ�һ�������������˶�ʱ�������P��PF��BC�ڵ�F�����ʡ�PDF���ܳ��Ƿ������ֵ������У�����������ֵ�����û�У���˵�����ɣ�
��3������P�����������˶�ʱ������CPD��ֱ��CP���ۣ���D�Ķ�Ӧ��Ϊ��Q�����ʣ��ı���CDPQ�Ƿ��Ϊ���Σ�����ܣ��������ʱ��P�����꣬������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com