
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.

【答案】(1) y=-x2+1;(2)①(2t,-1);②0<t≤![]() .
.
【解析】
(1)利用顶点式列出函数表达式,再将另一个点的坐标代入函数表达式列出一元一次方程,求出函数表达式.
(2)作出图象,结合图象思考.
解:(1)∵抛物线的顶点坐标为B(0,1)
∴设抛物线M的函数表达式为y=ax2+1
∵抛物线M经过点A(-1,0)
∴a×(-1)2+1=0,解得a=-1
∴抛物线M的函数表达为y=-x2+1
(2) ①由题意得,点F为BB1的中点
∵F(t,0),设B1的坐标为(m,n)
∴![]() ,
,![]()
∴m=2t,n=-1
∴B1(2t,-1).
②由题意可知抛物线M1的顶点B1的坐标为(2t,-1),二次项系数为1,
∴抛物线M1的函数表达式为:y=(x-2t)2-1(t>0),
当抛物线M1经过点A(-1,0)时(如下图):
∴(-1-2t)2-1=0,解得t1=-1,t2=0;

当抛物线M1经过点B(0,1)时(如上图):
∴(0-2t)2-1=1,解得t=![]() .
.
结合图象分析,因为t>0,所以当抛物线M1与线段AB有公共点时,t的取值范围是0<t≤![]() .
.
故答案为:(1) y=-x2+1;(2)①(2t,-1);②0<t≤![]() .
.


科目:初中数学 来源: 题型:
【题目】若一个三位数满足条件:其百位数字与十位数字之和为个位数字,则称这样的三位数为“吉祥数”,将“吉祥数”m的百位数字与个位数字交换位置,交换后所得的新数叫做m的“如意数”.如156是一个“吉祥数”,651是156的“如意数”.在吉祥数![]() 中当|x﹣y|=0或1时,称其为“和谐吉祥数”.
中当|x﹣y|=0或1时,称其为“和谐吉祥数”.
(1)个位数字为6的“和谐吉祥数”是 ,个位数字为9的“和谐吉祥数”是 .
(2)证明:任意一个“吉祥数”与其“如意数”之差都能被11整除;
(3)已知m为“吉祥数”,n是m的“如意数”,若m与n的和能被8整除,求m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() 、
、![]() 和点
和点![]() ,动点
,动点![]() 从原点
从原点![]() 开始沿
开始沿![]() 方向以每秒
方向以每秒![]() 个单位长度移动,动点
个单位长度移动,动点![]() 从点
从点![]() 开始沿
开始沿![]() 方向以每秒
方向以每秒![]() 个单位长度移动,动点
个单位长度移动,动点![]() 、
、![]() 同时出发,当动点
同时出发,当动点![]() 到达原点
到达原点![]() 时,点
时,点![]() 、
、![]() 停止运动.
停止运动.

![]() 直接写出抛物线的解析式:________;
直接写出抛物线的解析式:________;
![]() 求
求![]() 的面积
的面积![]() 与
与![]() 点运动时间
点运动时间![]() 的函数解析式;当
的函数解析式;当![]() 为何值时,
为何值时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
![]() 当
当![]() 的面积最大时,在抛物线上是否存在点
的面积最大时,在抛物线上是否存在点![]() (点
(点![]() 除外),使
除外),使![]() 的面积等于
的面积等于![]() 的最大面积?若存在,求出
的最大面积?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(5,0)和点B(0,4).


(1)求直线AB所对应的函数表达式;
(2)设直线y=x与直线AB相交于点C,求△BOC的面积;
(3)若将直线OC沿x轴向右平移,交y轴于点O′,当△AB O′为等腰三角形时,直接写出点O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班男同学身高情况如下表,则其中数据167cm( )
身高(cm) | 170 | 169 | 168 | 167 | 166 | 165 | 164 | 163 |
人数(人) | 1 | 2 | 5 | 8 | 6 | 3 | 3 | 2 |
A.是平均数B.是众数但不是中位数.
C.是中位数但不是众数D.是众数也是中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读数月活动中学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类)。下图是根据调查结果绘制的两幅不完整的统计图。

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中![]() ;
;
(3)扇形统计图中,艺术类读数所在扇形的圆心角是 度;
(4)学校计划购买课外读物8000册,请根据样本数据,估计学校购买其他类读数多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解决问题:已知a=![]() ,求2a2-8a+1的值,他是这样分析与解答的:
,求2a2-8a+1的值,他是这样分析与解答的:
因为a=![]() =
=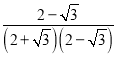 =2-
=2-![]() ,
,
所以a-2=-![]() .
.
所以(a-2)2=3,即a2-4a+4=3.
所以a2-4a=-1.
所以2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)计算: ![]() = - .
= - .
(2)计算:![]() +…+
+…+![]() ;
;
(3)若a=![]() ,求4a2-8a+1的值.
,求4a2-8a+1的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com