
 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )| A. | 20 | B. | $10\sqrt{2}$ | C. | 18 | D. | $20\sqrt{2}$ |
分析 设直角△AEF中,AE=x,则AF=x,EF=$\sqrt{2}$x,正八边形的边长是$\sqrt{2}$x.根据空白部分的面积是20即可列方程求得x的值,然后利用矩形和三角形的面积求解.
解答 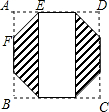 解:作出正方形ABCD.如图所示:
解:作出正方形ABCD.如图所示:
△AEF中,AE=x,则AF=x,EF=$\sqrt{2}$x,正八边形的边长是$\sqrt{2}$x.
则正方形的边长是(2+$\sqrt{2}$)x.
根据题意得:$\sqrt{2}$x(2+$\sqrt{2}$)x=20,
解得:x2=10($\sqrt{2}$-1).
则阴影部分的面积是:2[x(2+$\sqrt{2}$)x-2×$\frac{1}{2}$x2]=2($\sqrt{2}$+1)x2=2($\sqrt{2}$+1)×10($\sqrt{2}$-1)=20.
故选:A.
点评 本题考查了正多边形的计算,作出正方形,根据空白部分的面积,正确求得直角△AEF的直角边AE的长是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表| 成绩 | 划记 | 频数 | 百分比 |
| 优秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 | c | d | |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC在直角坐标系中的位置如图所示,直线l经过点(1,0),并且与x轴垂直,△A1B1C1与△ABC关于线l对称.
△ABC在直角坐标系中的位置如图所示,直线l经过点(1,0),并且与x轴垂直,△A1B1C1与△ABC关于线l对称.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A、B的坐标分别为(0,3)、(4,6),点P为x轴上的一个动点,若点B关于直线AP的对称点B′恰好落在坐标轴上,则点B′的坐标为(-4,0)(0,-2)(0,8).
如图,点A、B的坐标分别为(0,3)、(4,6),点P为x轴上的一个动点,若点B关于直线AP的对称点B′恰好落在坐标轴上,则点B′的坐标为(-4,0)(0,-2)(0,8).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com