
【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】AD 是ABC 中 BC 边上的中线,若 AB 3 , AD 4 ,则 AC 的取值范围是( )
A. 1 AC 7 B. 0.5 AC 3.5 C. 5 AC 11 D. 2.5 AC 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
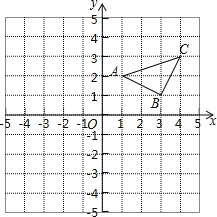
【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).
(1)作出 ![]() ABC关于原点O成中心对称的
ABC关于原点O成中心对称的 ![]() A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 ![]() A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
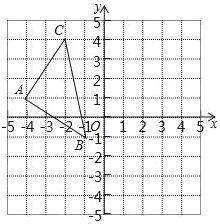
【题目】已知,△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )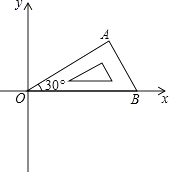
A.( ![]() ,﹣1)
,﹣1)
B.(1,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简.
(1)( x- y)( x+ y) ( x2+ y2) ( x4+ y4)·…·(x16+ y16);
(2)(22+1)(24+1)(28+1)(216+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的括号内:
-11,![]() ,3,
,3,![]() ,0,
,0,![]() ,
,![]() ,-12.101001…,-π,0.4.
,-12.101001…,-π,0.4.
有理数{ …};
无理数{ ……};
正实数{ …};
负实数{ ……}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
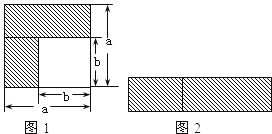
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,
(1) 作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标:
A1 ,B1 ,C1 .
(2) 直接写出△ABC的面积为 .
(3) 在x轴上画点P,使△PAC的周长最小. (不写作法,保留作图痕迹)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com