
 ��ͼ��������y=-$\frac{1}{2}$x2+bx+c��x��ֱ��ཻ�ڵ�A��-2��0����B��4��0������y�ύ�ڵ�C������Ϊ��P��
��ͼ��������y=-$\frac{1}{2}$x2+bx+c��x��ֱ��ཻ�ڵ�A��-2��0����B��4��0������y�ύ�ڵ�C������Ϊ��P������ ��1����A��-2��0����B��4��0��������������y=-$\frac{1}{2}$x2+bx+c�����b��c���ɣ�
��2���ٱ�ʾ��ON��MH������ON=MH���з�����⼴�ɣ�
�ڴ��ڣ������BC�Ľ���ʽ�����ݻ��ഹֱ��ֱ��һ����ϵ��������-1��ֱ�߾�����P������ϵ�������ֱ��PF�Ľ���ʽ����ֱ��BC��ֱ��PF�Ľ������꼴�ɣ�
��� �⣺��1����A��-2��0����B��4��0��������������y=-$\frac{1}{2}$x2+bx+c�ã�
$\left\{\begin{array}{l}{-2-2b+c=0}\\{-8+4b+c=0}\end{array}\right.$
��ã�b=1��c=4��
��y=-$\frac{1}{2}$x2+x+4��
��2����C��������0��4����B��4��0��
��ֱ��BC�Ľ���ʽΪy=-x+4��
�ٸ������⣬ON=OM=t��MH=-$\frac{1}{2}$t2+t+4
��ON��MH
�൱ON=MHʱ���ı���OMHNΪ���Σ�
��t=-$\frac{1}{2}$t2+t+4
��ã�t=2$\sqrt{2}$��t=-2$\sqrt{2}$������������ȥ��
��t=2$\sqrt{2}$����y=-$\frac{1}{2}$t2+t+4�ã�y=2$\sqrt{2}$
��H��2$\sqrt{2}$��2$\sqrt{2}$����
�ڴ��ڣ�
��PF��BCʱ��
��ֱ��BC�Ľ���ʽΪy=-x+4��
����PF�Ľ���ʽΪy=x+b���ֵ�P��1��$\frac{9}{2}$���������b=$\frac{7}{2}$��
����������з����飺
$\left\{\begin{array}{l}{y=-x+4}\\{y=x+\frac{7}{2}}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{x=\frac{1}{4}}\\{y=\frac{15}{4}}\end{array}\right.$
��F��$\frac{1}{4}$��$\frac{15}{4}$��
��PF��BPʱ��
�ߵ�P��1��$\frac{9}{2}$����B��4��0����
��ֱ��BP�Ľ���ʽΪ��y=-$\frac{3}{2}$x+6��
����PF�Ľ���ʽΪy=$\frac{2}{3}$x+b���ֵ�P��1��$\frac{9}{2}$���������b=$\frac{23}{6}$��
����������з����飺$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{2}{3}x+\frac{23}{6}}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{x=\frac{1}{10}}\\{y=\frac{39}{10}}\end{array}\right.$
��F��$\frac{1}{10}$��$\frac{39}{10}$����
������������PFBΪֱ��������ʱ����F������Ϊ��$\frac{1}{4}$��$\frac{15}{4}$����$\frac{1}{10}$��$\frac{39}{10}$����
���� ���⿼���˴���ϵ������ֱ�ߺ������߽���ʽ�������꣬���ε��ж��������Լ���ֱ���ഹֱ�����ʣ�������һ�����ۺ��ԣ��ѶȲ��ؼ���������ֱ���ഹֱ�����ʣ�


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
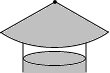 ��ͼ��Ҫ����һ��Բ�ε��̴�ñ��ʹ����Բ�İ뾶��ĸ�߳��ı���4��5����ô����������Ƥ��Բ�Ľ�ӦΪ��������
��ͼ��Ҫ����һ��Բ�ε��̴�ñ��ʹ����Բ�İ뾶��ĸ�߳��ı���4��5����ô����������Ƥ��Բ�Ľ�ӦΪ��������| A�� | 288�� | B�� | 144�� | C�� | 216�� | D�� | 120�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
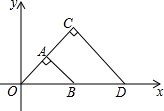 ��ͼ����OAB���OCD���Ե�OΪλ�����ĵ�λ��ͼ�Σ����Ʊ�Ϊ1��2����OCD=90�㣬CO=CD����B��1��0�������C������Ϊ��������
��ͼ����OAB���OCD���Ե�OΪλ�����ĵ�λ��ͼ�Σ����Ʊ�Ϊ1��2����OCD=90�㣬CO=CD����B��1��0�������C������Ϊ��������| A�� | ��1��2�� | B�� | ��1��1�� | C�� | ��$\sqrt{2}$��$\sqrt{2}$�� | D�� | ��2��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com