
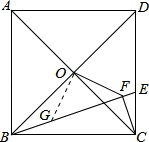
如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为__________.

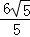 .
.
【考点】全等三角形的判定与性质;等腰直角三角形;正方形的性质.
【专题】计算题;几何图形问题.
【分析】在BE上截取BG=CF,连接OG,证明△OBG≌△OCF,则OG=OF,∠BOG=∠COF,得出等腰直角三角形GOF,在RT△BCE中,根据射影定理求得GF的长,即可求得OF的长.
【解答】解:如图,在BE上截取BG=CF,连接OG,
∵RT△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∵∠OBC=∠OCD=45°,
∴∠OBG=∠OCF,
在△OBG与△OCF中

∴△OBG≌△OCF(SAS)
∴OG=OF,∠BOG=∠COF,
∴OG⊥OF,
在RT△BCE中,BC=DC=6,DE=2EC,
∴EC=2,
∴BE=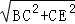 =
=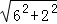 =2
=2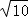 ,
,
∵BC2=BF•BE,
则62=BF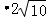 ,解得:BF=
,解得:BF=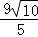 ,
,
∴EF=BE﹣BF= ,
,
∵CF2=BF•EF,
∴CF=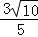 ,
,
∴GF=BF﹣BG=BF﹣CF=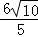 ,
,
在等腰直角△OGF中
OF2= GF2,
GF2,
∴OF=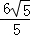 .
.
故答案为: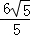 .
.
【点评】本题考查了全等三角形的判定和性质,直角三角形的判定以及射影定理、勾股定理的应用.


科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为 ,点C的坐标为
,点C的坐标为 ,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )
,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )
A.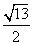 ;B.
;B. ; C.
; C. ;D.
;D. ;
;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )
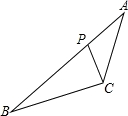
A.①②④ B.①③④ C.②③④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的口袋里装有标号为1,2,3,4,5的五个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球.
(1)下列说法:
①摸一次,摸出1号球和摸出5号球的概率相同;
②有放回的连续摸10次,则一定摸出2号球两次;
③有放回的连续摸4次,则摸出四个球标号数字之和可能是20.
其中正确的序号是__________.
(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com