
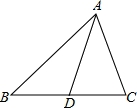
在△ABC中,AC=5cm,AD是△ABC中线,把△ABC周长分为两部分,若其差为3cm,则BA=__________.
8cm或2cm.
【考点】三角形的角平分线、中线和高.
【分析】先根据三角形中线的定义可得BD=CD,再求出AD把△ABC周长分为的两部分的差等于|AB﹣AC|,然后分AB>AC,AB<AC两种情况分别列式计算即可得解.
【解答】解:∵AD是△ABC中线,
∴BD=CD.
AD把△ABC周长分为的两部分分别是:AB+BD,AC+CD,
|(AB+BD)﹣(AC+CD)|=|AB﹣AC|=3,
如果AB>AC,那么AB﹣5=3,AB=8cm;
如果AB<AC,那么5﹣AB=3,AB=2cm.
故答案为:8cm或2cm.
【点评】本题考查了三角形的角平分线、中线和高线,熟记概念并求出AD把△ABC周长分为的两部分的差等于|AB﹣AC|是解题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
探究:
(1)如图①,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2__________∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2=__________;
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°﹣(∠B+∠C+∠1+∠2)=360°﹣__________=__________,猜想∠BDA+∠CEA与∠A的关系为__________.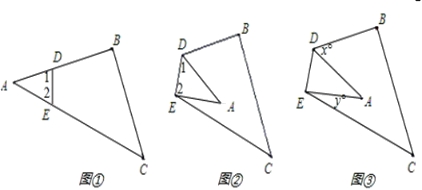
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出△APC≌△APD的是( )

A.BC=BD B.∠ACB=∠ADB C.AC=AD D.∠CAB=∠DAB
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB的垂线,交AC于E,交BC的延长线于F.
(1)∠1与∠B有什么关系?说明理由.
(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直角△ABD中,∠A=90°,AB=3cm,AD=9cm,将此三角形折叠,使点B与点D重合,折痕为EO,则△EOD的面积为__________cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
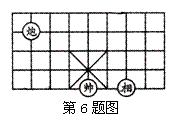
如图,是象棋盘的一部分,若帅位于点(1,-2)上,相位于点(3,-2),则炮位于点……………………………………………………………………………………( )
A.(-1,1); B.(-1,2); C.(-2,1); D.(-2,-2);
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com