
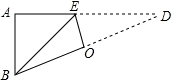
如图,直角△ABD中,∠A=90°,AB=3cm,AD=9cm,将此三角形折叠,使点B与点D重合,折痕为EO,则△EOD的面积为__________cm2.

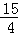 cm2.
cm2.
【考点】翻折变换(折叠问题).
【分析】设ED=xcm,则AE=(9﹣x)cm,由翻折的性质可知:S△EBO=S△EDO,BE=ED=x,在Rt△AEB中,由勾股定理可求得DE=5,然后根据S△EOD=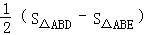 求解即可.
求解即可.
【解答】解:设ED=xcm,则AE=(9﹣x)cm,由翻折的性质可知:BE=ED=x.
在Rt△AEB中,由勾股定理可知:BE2=AE2+AB2,即x2=(9﹣x)2+32,
解得:x=5.
∴ED=5cm.
由翻折的性质可知:S△EBO=S△EDO.
∵S△EBO=S△EDO,
∴S△EOD=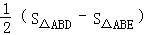 =
=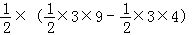 =
=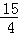 .
.
故答案为: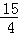 .
.
【点评】本题主要考查的是翻折的性质,利用翻折的性质、勾股定理列出关于x的方程是解题的关键.


科目:初中数学 来源: 题型:
如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
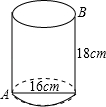
A.20cm B.30cm C.40cm D.50cm
查看答案和解析>>
科目:初中数学 来源: 题型:
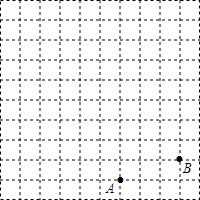
如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
(1)建立适当的平面直角坐标系,使点A,点B的坐标分别为(1,﹣4)(4,﹣3);
(2)点C的坐标为(2,﹣2),在平面直角坐标系中标出点C的位置,连接AB,BC,CA,则△ABC是__________三角形;
(3)在图中作出△ABC关于x轴对称的图形△A1B1C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
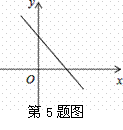
已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是…………………( )
A.m>0,n<3; B.m>0,n>3; C.m<0,n<3; D.m<0,n>3;
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com