
如图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB的垂线,交AC于E,交BC的延长线于F.
(1)∠1与∠B有什么关系?说明理由.
(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由.

【考点】全等三角形的判定与性质.
【专题】探究型.
【分析】(1)∠ACB=90°,∠1+∠F=90°,又由于DF⊥AB,∠B+∠F=90°,继而可得出∠1=∠B;
(2)通过判定△ABC≌△FBD(ASA),可得出AB=FB.
【解答】解:(1)∠1=∠B
理由:由∠ACB=90°,知∠1+∠F=90°
又DF⊥AB,所以∠B+∠F=90°
则∠1=∠B
(2)AB=FB
理由:在△ABC和△FBD中,
∵∠ACB=∠FDB=90°,BC=BD,∠B=∠B,
∴△ABC≌△FBD,
∴AB=FB.
【点评】本题考查全等三角形的判定与性质,难度适中,关键是熟练掌握全等三角形的判定方法.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
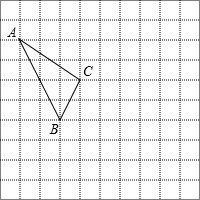
在如图所示的正方形网格中,每 个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(3)写出点B的坐标__________;
(2)请求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
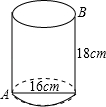
A.20cm B.30cm C.40cm D.50cm
查看答案和解析>>
科目:初中数学 来源: 题型:
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNK T的面积分别为
T的面积分别为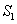 、
、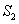 、
、 .若正方形EFGH的边长为2,则
.若正方形EFGH的边长为2,则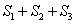 = .
= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com