
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为__________度.
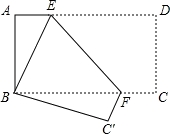
125度.
【考点】翻折变换(折叠问题).
【分析】由折叠的性质知:∠EBC′、∠BC′F都是直角,因此BE∥C′F,那么∠EFC′和∠BEF互补,欲求∠EFC′的度数,需先求出∠BEF的度数;根据折叠的性质知∠BEF=∠DEF,而∠AEB的度数可在Rt△ABE中求得,由此可求出∠BEF的度数,即可得解.
【解答】解:Rt△ABE中,∠ABE=20°,∴∠AEB=70°;
由折叠的性质知:∠BEF=∠DEF;
而∠BED=180°﹣∠AEB=110°,∴∠BEF=55°;
易知∠EBC=∠D=∠BC′F=∠C=90°,
∴BE∥C′F,
∴∠EFC′=180°﹣∠BEF=125°.
【点评】本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
在一个不透明的口袋里装有标号为1,2,3,4,5的五个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球.
(1)下列说法:
①摸一次,摸出1号球和摸出5号球的概率相同;
②有放回的连续摸10次,则一定摸出2号球两次;
③有放回的连续摸4次,则摸出四个球标号数字之和可能是20.
其中正确的序号是__________.
(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
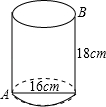
A.20cm B.30cm C.40cm D.50cm
查看答案和解析>>
科目:初中数学 来源: 题型:
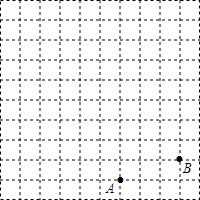
如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
(1)建立适当的平面直角坐标系,使点A,点B的坐标分别为(1,﹣4)(4,﹣3);
(2)点C的坐标为(2,﹣2),在平面直角坐标系中标出点C的位置,连接AB,BC,CA,则△ABC是__________三角形;
(3)在图中作出△ABC关于x轴对称的图形△A1B1C1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com