如图：BO、CO是∠ABC，∠ACB的两条角平分线，∠A=100°，则∠BOC的度数为( )
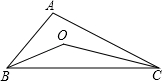
A．80° B．90° C．120° D．140°
D【考点】角平分线的定义；三角形内角和定理．
【分析】△ABC中，已知∠A即可得到∠ABC与∠ACB的和，而BO、CO是∠ABC，∠ACB的两条角平分线，即可求得∠OBC与∠OCB的度数，根据三角形的内角和定理即可求解．
【解答】解：△ABC中，∠ABC+∠ACB=180°﹣∠A=180°﹣100°=80°，
∵BO、CO是∠ABC，∠ACB的两条角平分线．
∴∠OBC=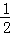
∠ABC，∠OCB=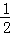∠ACB，
∴∠OBC+∠OCB=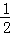（∠ABC+∠ACB）=40°，
在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）=140°．
故选D．
【点评】本题主要考查了三角形的内角和定理，以及三角形的角平分线的定义．
科目：初中数学 来源： 题型：
如图，是由一些棱长为单位1的相同的小正方体组合成的简单几何体．
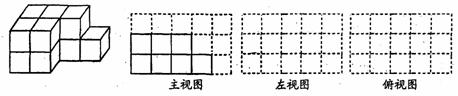
(1)图中有 块小正方体；
(2)请在相应方格纸中分别画出几何体的左视图和俯视图；
(3)如果在其表面涂漆，则要涂 平方单位．（几何体放在地上，底面无法涂上漆）
查看答案和解析>>
科目：初中数学 来源： 题型：
已知，如图△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连接DH与BE相交于点G，某同学分析图形后得出以下结论：①DH⊥BC；②CE=
；③△AEB≌△CEB；④△BDF≌△CDA．上述结论一定正确的是( )
A．①③ 
B．③④ C．①③④ D．①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
正数a的正的平方根叫做a的算术平方根，记作：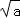
，我们把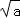≥0和a≥0叫做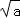的两个非负性，据此解决以下问题：
（1）若实数a、b满足
=0，求a+b的立方根．
（2）已知实数x、y满足y=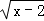
+
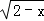+2，求xy的平方根．
查看答案和解析>>
科目：初中数学 来源： 题型：
探究：
（1）如图①，∠1+∠2与∠B+∠C有什么关系？为什么？
（2）把图①△ABC沿DE折叠，得到图②，填空：∠1+∠2__________∠B+∠C（填“＞”“＜”“=”），当∠A=40°时，∠B+∠C+∠1+∠2=__________；
（3）如图③，是由图①的△ABC沿DE折叠得到的，如果∠A=30°，则x+y=360°﹣（∠B+∠C+∠1+∠2）=360°﹣__________=__________，猜想∠BDA+∠CEA与∠A的关系为__________．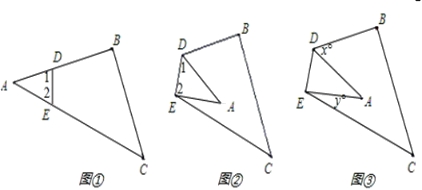
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
