
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE= ;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )

A.①③  B.③④ C.①③④ D
B.③④ C.①③④ D .①②③④
.①②③④
D【考点】全等三角形的判定与性质.
【分析】根据∠ABC=45°,CD⊥AB于D,可以证明△BCD是等腰直角三角形,然后根据等腰直角三角形的性质可得DH⊥BC,判断①正确,然后证明△BDF与△CDA全等,④正确,根据全等三角形对应边相等可得BF=AC,根据BE平分∠ABC,且BE⊥AC于E,可以证明△ABE与△CBE全等,③正确;根据全等三角形对应边相等可得AE=CE,从而判断②正确.
【解答】解:∵∠ABC=45°,CD⊥AB于D,
∴△BCD是等腰直角三角形,H是BC边的中点,
∴BD=CD,DH⊥BC,①正确;
∵CD⊥AB于D,BE⊥AC于E,
∴∠DBF+∠A=90°,∠ACD+∠A=90°,
∴∠DBF=∠ACD,
在△BDF与△CDA中,
 ,
,
∴△BDF≌△CDA(ASA),故④正确;
∴BF=AC,
∵BE平分∠ABC,且BE⊥AC于E,
∴∠ABE=∠CBE,∠AEB=∠CEB=90°,
∴在△ABE与△CBE中,
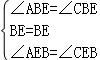 ,
,
∴△ABE≌△CBE(ASA),故③正确;
∴AE=CE=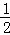 AC,
AC,
∴BF=2CE,故②正确;
【点评】本题考查了等腰直角三角形的判定与性质,角平分线的性质,全等三角形的判定与性质,仔细分析图形并熟练掌握各性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
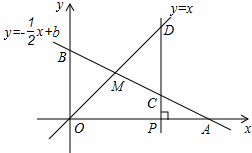
如图,已知函数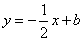 的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P
的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P 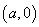 (其中
(其中 >2),过点P作x轴的垂线,分别交函数
>2),过点P作x轴的垂线,分别交函数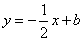 和
和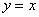 的图象于点C、D.
的图象于点C、D.
 (1)求点A的坐标;
(1)求点A的坐标;
(2)若OB=CD,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )
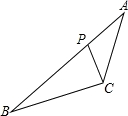
A.①②④ B.①③④ C.②③④ D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的口袋里装有标号为1,2,3,4,5的五个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球.
(1)下列说法:
①摸一次,摸出1号球和摸出5号球的概率相同;
②有放回的连续摸10次,则一定摸出2号球两次;
③有放回的连续摸4次,则摸出四个球标号数字之和可能是20.
其中正确的序号是__________.
(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一个圆桶儿,底面直径为16cm,高为18cm,则一只小虫底部点A爬到上底B处,则小虫所爬的最短路径长是(π取3)( )
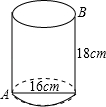
A.20cm B.30cm C.40cm D.50cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com