
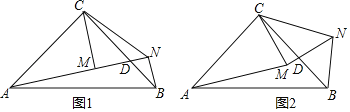
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,以C为顶点作等腰直角三角形CMN.使∠CMN=90°,连接BN,射线NM交BC于点D.
(1)如图1,若点A,M,N在一条直线上,
①求证:BN+CM=AM;
②若AM=4,BN=![]() ,求BD的长;
,求BD的长;
(2)如图2,若AB=4,CN=2,将△CMN绕点C顺时针旋转一周,在旋转过程中射线NM交AB于点H,当三角形DBH是直角三角形时,请你直接写出CD的长.
【答案】(1)①证明见解析;②![]() ;(2)2.
;(2)2.
【解析】
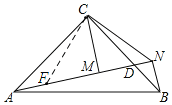
(1)①如图,过点C作CF⊥CN,交AN于点F,由等腰直角三角形的性质,可求∠CNM=45°,CM=MN,即可证∠FCN=∠ACB,∠CFN=∠CNF=45°,根据“SAS”可证
△ACF≌△BCN,可得AF=BN,根据等腰直角三角形的性质可得MF=MN=CM,即可证BN+CM=AM;
②由题意可求出CM=MN=![]() ,由全等三角形的性质可得∠CAF=∠CBN,即可证∠MCD=∠CBN,则CM∥BN,可得△MCD∽△NBD,根据相似三角形的性质和勾股定理可求BD的长;
,由全等三角形的性质可得∠CAF=∠CBN,即可证∠MCD=∠CBN,则CM∥BN,可得△MCD∽△NBD,根据相似三角形的性质和勾股定理可求BD的长;
(2)分∠BDH=90°,∠DHB=90°两种情况讨论,根据等腰直角三角形的性质可求CD的长.
证明:(1)①如图,过点C作CF⊥CN,交AN于点F,
∵△CMN是等腰直角三角形,
∴∠CNM=45°,CM=MN,
∵CF⊥CN,∠ACB=90°,
∴∠FCN=∠ACB,∠CFN=∠CNF=45°,
∴∠ACF=∠BCN,CF=CN,且AC=BC,
∴△ACF≌△BCN(SAS),
∴AF=BN,
∵CF=CN,CM⊥MN,
∴MF=MN=CM,
∴AM=AF+FM=BN+CM
②∵AM=4,BN=![]() ,BN+CM=AM,
,BN+CM=AM,
∴CM=MN=![]() ,
,
∵△ACF≌△BCN,
∴∠CAF=∠CBN,
∵∠CAF+∠ACF=∠CFN=45°,∠BCN+∠MCD=∠MCN=45°
∴∠CAF=∠MCD,且∠CAF=∠CBN,
∴∠MCD=∠CBN
∴CM∥BN
∴△MCD∽△NBD,∠CMD=∠BND=90°
∴![]() =
=![]()
∴MD=![]() ND
ND
∵MD+ND=MN=![]()
∴ND=![]()
在Rt△DNB中,BD=![]() =
=![]()
(2)若∠BDH=90°,如图,此时点M与点D重合,
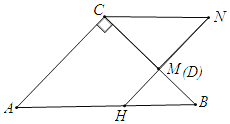
∵△CMN是等腰直角三角形,CN=2
∴CM=MN=![]()
∴CD=![]() ,
,
若∠BHD=90°,如图,
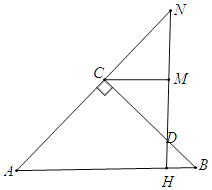
∵∠BHD=90°,∠B=45°,
∴∠BDH=45°
∴∠CDN=45°=∠N
∴CD=CN=2.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】为迎接国庆节,某商店购进了一批成本为每件30元的纪念商品.经调查发现,该商品每天的销售量![]() (件
(件![]() 与销售单价
与销售单价![]() (元
(元![]() 满足一次函数关系,其图象如图所示.
满足一次函数关系,其图象如图所示.

(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)若商店按不低于成本价,且不高于60元的单价销售,则销售单价定为多少,才能使销售该商品每天获得的利润![]() (元
(元![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某公园一圆形喷水池,在池中心竖直安装一根水管OA=1.25m,A处是喷头,水流在各个方向沿形状相同的抛物线落下,水落地后形成一个圆,圆心为O,直径为线段CB.建立如图所示的平面直角坐标系,若水流路线达到最高处时,到x轴的距离为2.25m,到y轴的距离为1m,则水落地后形成的圆的直径CB=_____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,BE=EC,将正方形ABCD的边CD沿DE折叠到DF,连接EF、FC、FB,若△DFC的面积为16,则△BEF的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
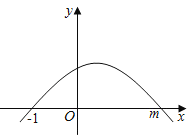
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
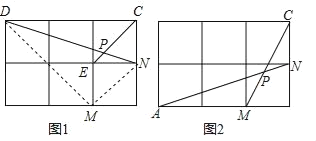
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
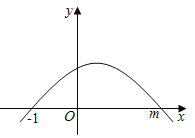
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com