
分析 (1)、(2)、(3)先根据分式的加法法则把原式进行化简,再把ab=1代入进行计算即可.
解答 解:(1)原式=$\frac{a(1+b)+b(1+a)}{(1+a)(1+b)}$
=$\frac{a+ab+b+ab}{1+a+b+ab}$
=$\frac{2+a+b}{2+a+b}$
=1;
(2)原式=$\frac{1+{b}^{2}+1+{a}^{2}}{(1+{a}^{2})(1+{b}^{2})}$
=$\frac{2+{a}^{2}+{b}^{2}}{1+{b}^{2}+{a}^{2}+{a}^{2}{b}^{2}}$
=$\frac{2+{a}^{2}+{b}^{2}}{2+{b}^{2}+{a}^{2}}$
=1;
(3)原式=$\frac{1+{b}^{n}+1+{a}^{n}}{(1+{a}^{n})(1+{b}^{n})}$
=$\frac{2+{a}^{n}+{b}^{n}}{1+{b}^{n}+{a}^{n}+{a}^{n}{b}^{n}}$
=$\frac{2+{a}^{n}+{b}^{n}}{2+{b}^{n}+{a}^{n}}$
=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{9}$ | D. | $\root{3}{-\frac{1}{27}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
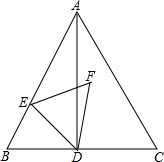 已知等边△ABC的边长为4,点D是边BC的中点,点E在线段BA上由点B向点A运动,连接ED,以ED为边在ED右侧作等边三角形EDF,设△EDF的中心为O,则点E由点B向点A运动的过程中,点O运动的路径长为$\frac{4\sqrt{3}}{3}$.
已知等边△ABC的边长为4,点D是边BC的中点,点E在线段BA上由点B向点A运动,连接ED,以ED为边在ED右侧作等边三角形EDF,设△EDF的中心为O,则点E由点B向点A运动的过程中,点O运动的路径长为$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com