
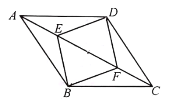
【题目】如图,E,F是菱形ABCD对角线上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若![]() ,AD=6,AE=DE,求菱形BEDF的周长
,AD=6,AE=DE,求菱形BEDF的周长
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接BD,由菱形ABCD的性质得出OA=OC,OB=OD,AC⊥BD,得出OE=OF,证出四边形BEDF是平行四边形,再由EF⊥BD,即可证出四边形BEDF是菱形;
(2)求出∠DAE=30°,得出![]() 再证出∠ADE=∠EDO=30°,在Rt△DEO中,由三角函数求出
再证出∠ADE=∠EDO=30°,在Rt△DEO中,由三角函数求出![]() 即可得出菱形BEDF的周长.
即可得出菱形BEDF的周长.
(1)证明:连接BD,交AC于O,如图所示:
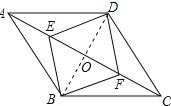
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
(2)∵![]()
∴![]()
∵AD=6,
∴![]()
∵AE=DE,
∴![]()
在Rt△DEO中, ![]()
∴菱形BEDF的周长![]()


科目:初中数学 来源: 题型:
【题目】已知双曲线![]() 与直线
与直线![]() 交于A、B两点,点A的坐标为(3,2).
交于A、B两点,点A的坐标为(3,2).
(1)由题意可得![]() 的值为______,
的值为______,![]() 的值为________,点B的坐标为_________;
的值为________,点B的坐标为_________;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)若点P![]() 在第一象限的双曲线上,试求出
在第一象限的双曲线上,试求出![]() 的值及点P的坐标。
的值及点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
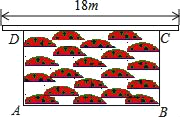
【题目】2018年,汶上县县委、县政府启动创建全国卫生县城和全国文明县城工作,各单位都积极投身创城工作某单位为进一步美化我县环境,在临街的围墙外靠墙摆设一长方形花圃景观,花圃一边靠墙,墙长18m,外围用40m的栅栏围成,如图所示,若设花圃的BC边长为x(m),花圃的面积为y(m2).
(1)求出y与x之间的函数关系式,并写出自变量x的取值范围;
(2)利用所学知识试着求出花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
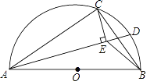
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
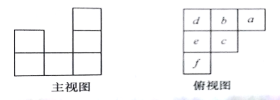
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)求![]() 的值;
的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当![]() 时画出这个几何体的左视图.
时画出这个几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
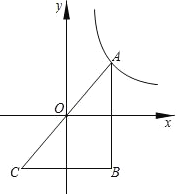
【题目】已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求w的取值范围;
(2)点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,若△ABC的面积为4,求w的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2x+k=0.
(1)若方程有实数根,求k的取值范围;
(2)如果k是满足条件的最大的整数,且方程x2-2x+k=0一根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,求m的值及这个方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
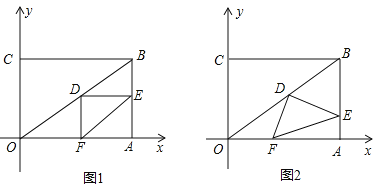
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
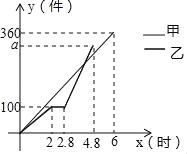
【题目】甲、乙两组工人同时开始加工某种零件,乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)之间的函数图象如图所示.甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过_____小时恰好装满第1箱.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com