
【题目】如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N的坐标为(m,n).

(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为 ,点C的坐标为 ;请直接写出点N纵坐标n的取值范围是 ;
(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.(提示:连结MN,![]() ,
,![]() )
)
【答案】(1)D(1,0),C(0,﹣1);0<n≤![]() ;(2)EC=
;(2)EC=![]() +
+![]() ,AM+BM+CM的最小值为
,AM+BM+CM的最小值为![]() +
+![]()
【解析】
(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,根据正方形的性质得到OA=OB=OC=OD,由点B(1,0),A(0,1),于是得到D(1,0),C(0,1);过N作NH⊥BD于h,根据旋转的性质得到∠NBH=60°,BM=BN,求得NH=![]() BN=
BN=![]() t,于是得到结论;
t,于是得到结论;
(2)如图所示,连接MN,过E作EH⊥BC,交CB的延长线于H,由旋转的性质得到BM=BN,∠NBM=60°,求得△BMN是等边三角形,求得MN=BM,根据等边三角形的性质得到BE=BA,∠ABE=60°,求得∠ABM=∠EBN,根据全等三角形的性质得到AM=EN,求得AM+BM+CM=EN+MN+CM,当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,利用勾股定理即可得到结论.
解:(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,
∵点B(﹣1,0),A(0,1),
∴D(1,0),C(0,﹣1);
过N作NH⊥BD于h,
∴∠NHB=90°,
∵将BM绕点B逆时针旋转60°得到BN,
∴∠NBH=60°,BM=BN,
∴NH=![]() BN=
BN=![]() t,
t,
∵0<t≤2,
∴点N纵坐标n的取值范围是0<n≤![]() ;
;
(2)如图2所示,连接MN,过E作EH⊥BC,交CB的延长线于H,
由旋转可得,BM=BN,∠NBM=60°,
∴△BMN是等边三角形,
∴MN=BM,
∵△ABE是等边三角形,
∴BE=BA,∠ABE=60°,
∴∠ABM=∠EBN,
∴△ABM≌△EBN(SAS),
∴AM=EN,
∴AM+BM+CM=EN+MN+CM,
∴当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,
又∵∠ABE=60°,∠ABH=90°,
∴∠EBH=30°,
∴Rt△EBH中,EH=![]() EB=
EB=![]() ×2=1,
×2=1,
∴BH=![]() =
=![]() =
=![]() ,
,
∴CH=2+![]() ,
,
∴Rt△CEH中,CE=![]() =
=![]() =
=![]() =
=![]() ;
;
∴AM+BM+CM的最小值为![]() +
+![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】养成良好的早锻炼习惯,对学生的学习和生活都非常有益,某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间x(分钟)进行了调查.现把调查结果分成A、B、C、D四组,如下表所示,同时,将调查结果绘制成下面两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在 区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
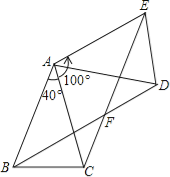
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整.
解:∵DE∥BC(已知)
∴______(两直线平行,内错角相等)
∵EF∥AB(已知)
∴∠ABC=∠EFC(______)
∴∠DEF=∠ABC=40°(等量代换)
应用:如图2,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线R上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=50°,求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=mx+1的图象经过点A(﹣1,0),且与反比例函数![]() (k≠0)交于点B(n,2).
(k≠0)交于点B(n,2).
(1)求一次函数的解析式
(2)求反比例函数的解析式
(3)直接写出求当1≤x≤6时,反比例函数y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ∥
∥![]() ,直线
,直线![]() 和
和![]() ,
,![]() 分别交于点
分别交于点![]() .A为
.A为![]() 上一点,B为
上一点,B为![]() 上一点,P为
上一点,P为![]() 上一动点。
上一动点。
(1)如果P在C、D之间运动,如图①(点P与点C、D不重合),请说明:![]()
(2)如果P在CD两点的外侧运动,如图②、图③(点P与点C、D不重合),问∠APB,![]() ,
,![]() 有何关系,请直接写出结论。
有何关系,请直接写出结论。



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
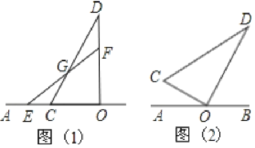
【题目】如图,已知点O在直线AB上,将一副直角三角板的直角顶点放在点O处,其中∠OCD=60°,∠OEF=45°.边OC、OE在直线AB上.
(1)如图(1),若CD和EF相交于点G,则∠DGF的度数是______°;
(2)将图(1)中的三角板OCD绕点O顺时针旋转30°至图(2)位置
①若将三角板OEF绕点O顺时针旋转180°,在此过程中,当∠COE=∠EOD=∠DOF时,求∠AOE的度数;
②若将三角板OEF绕点O以每秒4°的速度顺时针旋转180°,与此同时,将三角板OCD绕点O以每秒1°的速度顺时针旋转,当三角板OEF旋转到终点位置时,三角板OCD也停止旋转.设旋转时间为t秒,当OD⊥EF时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=900,点A、C的坐标分别为A(-2,0),C(1,0),tan∠BAC=![]() .
.
(1)求点B的坐标。
(2)在x轴上找一点D,连接DB,使得△BCD与△ABC相似(不包括全等),并求点D的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一次函数y=(2m-1)x+m -2,若它的函数值y随x的增大而增大,且图象与y轴负半轴相交,且m为正整数.
(1)求这个函数的解析式.
(2)求直线y=-x和(1)中函数的图象与x轴围成的三角形面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com