
【题目】探究:如图1,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整.
解:∵DE∥BC(已知)
∴______(两直线平行,内错角相等)
∵EF∥AB(已知)
∴∠ABC=∠EFC(______)
∴∠DEF=∠ABC=40°(等量代换)
应用:如图2,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线R上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,若∠ABC=50°,求∠DEF的度数.

【答案】探究:∠DEF=∠EFC;两直线平行,同位角相等;应用:130°.
【解析】
(1)依据两直线平行,内错角相等;两直线平行,同位角相,即可得到∠DEF=40°.
(2)依据两直线平行,内同位角相;两直线平行,同旁内角互补,即可得到∠DEF=180°-50°=130°.
解:(1)∵DE∥BC,
∴∠DEF=∠EFC.(两直线平行,内错角相等)
∵EF∥AB,
∴∠EFC=∠ABC.(两直线平行,同位角相等)
∴∠DEF=∠ABC=40°.(等量代换)
故答案为:∠DEF=∠EFC;两直线平行,同位角相等;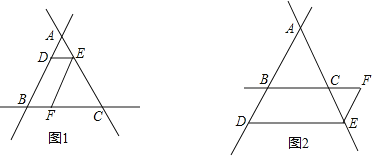
(2)∵DE∥BC,
∴∠ABC=∠EADE=50°.(两直线平行,内同位角相等)
∵EF∥AB,
∴∠ADE+∠DEF=180°.(两直线平行,同旁内角互补)
∴∠DEF=180°-50°=130°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程x2﹣6x﹣m=0有两个实数根.
(1)求m的取值范围;
(2)如果m取符合条件的最小整数,且一元二次方程x2﹣6x﹣m=0与x2+nx+1=0有一个相同的根,求常数n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
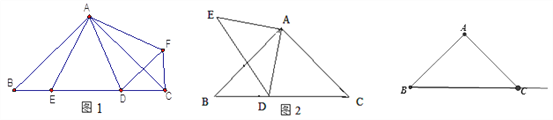
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
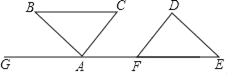
【题目】如图,点A、F在线段GE上,AB∥DE,BC∥GE,AC∥DF,AB=DE
(1)请说明:△ABC≌△DEF;
(2)连接BF、CF、CE,请你判断BF与CE之间的关系?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=4cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则以下结论:①AD平分∠CDE;②DE平分∠BDA;③AE-BE=BD;④△BDE周长是4cm.其中正确的有( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形.
(1)利用尺规作∠ABC的平分线BE,交AD于E(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求证:AB=AE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N的坐标为(m,n).

(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为 ,点C的坐标为 ;请直接写出点N纵坐标n的取值范围是 ;
(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.(提示:连结MN,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣20)+(+3)﹣(﹣5)
(2)(﹣5)×6×![]() ÷(﹣2)
÷(﹣2)
(3)﹣![]() ÷
÷![]() ﹣
﹣![]() ×(﹣9)
×(﹣9)
(4)(﹣1)4+5÷(﹣![]() )×(﹣6)
)×(﹣6)
(5)(![]() +
+![]() ﹣
﹣![]() )×36
)×36
(6)﹣1﹣[1![]() +(﹣12)÷6]×(﹣
+(﹣12)÷6]×(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置……,则正方形铁片连续旋转2020次后,点P的坐标为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com