
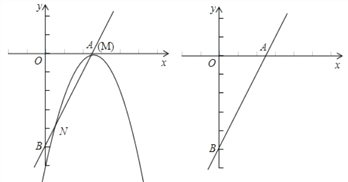
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,抛物线y=-x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=-x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式![]() ;
;
(2)点N的坐标为![]() ,线段MN的长为
,线段MN的长为![]() ;
;
(3)存在点M(2,-1),或(4,3)
【解析】试题分析:(1)①首先求得直线与x轴,y轴的交点坐标,利用二次函数的对称轴的公式即可求解;
②N在直线上同时在二次函数上,因而设N的横坐标是a,则在两个函数上对应的点的纵坐标相同,据此即可求得a的值,即N的坐标,过N作NC⊥x轴,垂足为C,利用勾股定理即可求得MN的长;
(2)△AOB的三边长可以求得OB=2OA,AB边上的高可以求得是![]() ,抛物线y=-x2+bx+c在直线AB上平移,则MN的长度不变,根据(1)的结果是2
,抛物线y=-x2+bx+c在直线AB上平移,则MN的长度不变,根据(1)的结果是2![]() ,MN是AB边上的高的二倍,当OM⊥AB或ON⊥AB时,两个三角形相似,据此即可求得M的坐标.
,MN是AB边上的高的二倍,当OM⊥AB或ON⊥AB时,两个三角形相似,据此即可求得M的坐标.
试题解析:(1)①∵直线y=2x-5与x轴和y轴交于点A和点B,
∴A(![]() ,0),B(0,-5).
,0),B(0,-5).
当顶点M与点A重合时,
∴M(![]() ,0).
,0).
∴抛物线的解析式是:y=(x![]() )2.即y=x2+5x
)2.即y=x2+5x![]() .
.
②∵N在直线y=2x-5上,设N(a,2a-5),又N在抛物线y=x2+5x![]() 上,
上,
∴2a5=a2+5a![]() .
.
解得a1=![]() ,a2=
,a2=![]() (舍去)
(舍去)
∴N(![]() ,4).
,4).
过N作NC⊥x轴,垂足为C.
∵N(![]() ,4),
,4),
∴C(![]() ,0).
,0).
∴NC=4.MC=OMOC=![]()
![]() =2.
=2.
∴MN=![]() ;
;
(2)设M(m,2m-5),N(n,2n-5).
∵A(![]() ,0),B(0,-5),
,0),B(0,-5),
∴OA=![]() ,OB=5,则OB=2OA,AB=
,OB=5,则OB=2OA,AB=![]() ,
,
当∠MON=90°时,∵AB≠MN,且MN和AB边上的高相等,因此△OMN与△AOB不能全等,
∴△OMN与△AOB不相似,不满足题意.
当∠OMN=90°时, ![]() ,即
,即![]() ,解得OM=
,解得OM=![]() ,
,
则m2+(2m-5)2=(![]() )2,解得m=2,
)2,解得m=2,
∴M(2,-1);

当∠ONM=90°时, ![]() ,即
,即![]() ,解得ON=
,解得ON=![]() ,
,
则n2+(2n-5)2=(![]() )2,解得n=2,
)2,解得n=2,
∵OM2=ON2+MN2,
即m2+(2m-5)2=5+(2![]() )2,
)2,
解得:m=4,
则M的坐标是M(4,3).
故M的坐标是:(2,-1)或(4,3).


科目:初中数学 来源: 题型:
【题目】如图,小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.
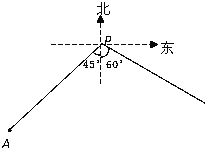
(1)出发后几小时两船与港口P的距离相等;
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月29日,新建的无锡文化旅游城将盛大开业,开业后预计接待游客量约20 000 000 人次,这个年接待课量可以用科学记数法表示为________人次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A. 平均数B. 中位数C. 方差D. 标准差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com