
����Ŀ����ͼ��С��A�ڸۿ�P����ƫ��45��������ۿ�81���ﴦ���״���A��������AP������9����/ʱ���ٶ�ʻ��ۿڣ��Ҵ��Ӹۿ�P����������ƫ��60��������18����/ʱ���ٶ�ʻ��ۿڣ�������ͬʱ������
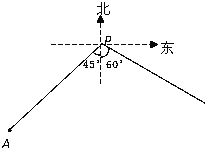
��1��������Сʱ������ۿ�P�ľ�����ȣ�
��2��������Сʱ�Ҵ��ڼ״����������������ȷ��0��1Сʱ�����ο����ݣ�![]() ��1��41��
��1��41��![]() ��1��73��
��1��73��
���𰸡���1��3����2��Լ3��7��
��������
���������������Ӧ���⣻ѹ�������ڴ����˶������У�������ֱ�������ε����⣬����ѧ������ѧ֪ʶ�ı�ʽ��ʶ������
��1����Сʱ��������ۿڵľ�����ȣ�����ת��Ϊ���̵���������
��2������P��PE��CD������ΪE�����E�ڵ�P�����Ϸ�����õ���ȹ�ϵ��C��D���㵽���ϱ������Ͼ����ľ�����ȣ�������ݷ��̾Ϳ��Խ����
���������
�⣺��1���������xСʱ������ۿ�P�ľ��������
���������81��9x=18x��
��������̵�x=3��
�𣺳�����3Сʱ������ۿ�P�ľ��������
��2���������yСʱ�Ҵ��ڼ״�����������
��ʱ�ס���������λ�÷ֱ��ڵ�C��D����
����CD������P��PE��CD������ΪE��
���E�ڵ�P�����Ϸ�����
��Rt��CEP����CPE=45����
��PE=PCcos45����
��Rt��PED����EPD=60����
��PE=PDcos60����
��PCcos45��=PDcos60����
����81��9y��cos45��=18ycos60����
���y��3��7��
�𣺳�����Լ3��7Сʱ�Ҵ��ڼ״�������������



 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA��3��OC��2��F��AB�ϵ�һ������(F����A��B�غ�)������F�ķ���������y��![]() (x��0)��ͼ����BC�߽��ڵ�E.
(x��0)��ͼ����BC�߽��ڵ�E.
(1)��FΪAB���е�ʱ����ú����Ľ���ʽ��
(2)��kΪ��ֵʱ����EFA���������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����涨m��n=mn��m��n������a+b������a��b����ֵ�� ��
A.2ab2��2b2
B.2a2b��2b3
C.2a2b+2b2
D.2ab��2ab2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ����ཻ�ڵ�O����AB��AD����O��OE��BD��BC�ڵ�E������CDE���ܳ�Ϊ10����ƽ���ı���ABCD���ܳ�Ϊ �� 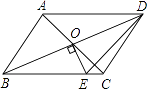
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2��2x=0�ĸ��ǣ� ��
A.x1=0��x2=��2
B.x1=1��x2=2
C.x1=1��x2=��2
D.x1=0��x2=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
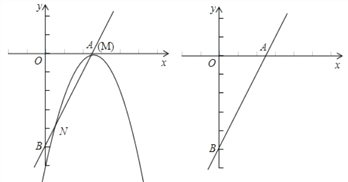
����Ŀ����ֱ֪��y=2x-5��x���y��ֱ��ڵ�A�͵�B��������y=-x2+bx+c�Ķ���M��ֱ��AB��,����������ֱ��AB����һ������ΪN��
��1����ͼ,����M���A�غ�ʱ���������ߵĽ���ʽ��
��2���ڣ�1���������£����N��������߶�MN�ij���
��3��������y=-x2+bx+c��ֱ��AB��ƽ��,�Ƿ���ڵ�M,ʹ�á�OMN���AOB����?������,ֱ��д����M�����ꣻ��������,��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڳ��ֽ���ʽ����Ŀʱ����С��©���˶���ʽx2����y2(��������ʾ©����ʽ��)��y2ǰ��ʽ�ӣ��Ҹö���ʽ�ֽܷ���ʽ����ô��©������ҵ���ϵ�ʽ�Ӳ������������е�( �� )
A. x B. 4 C. ��4 D. 9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӡ�O��һ��A����O������AB,�е�ΪB,����AO���ӳ�����O�ڵ�C,��D.����BC.
(1)��ͼ1������A=26�������C�Ķ�����
(2)��ͼ2����AEƽ�֡�BAC,��BC�ڵ�E.���AEB�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ҹ��Ŵ���ѧ��������緢�ֵģ���Ϊ��������ǡ������ķ��ֱ�����Ҫ����������ң��ɴ˿ɼ��ҹ��Ŵ���ѧ�ijɾ��Ƿdz�ֵ���л������Ժ��ģ���������ǡ�����������ɣ�������ÿһ�е��������ö�Ӧ�ˣ�a+b��n��nΪ�Ǹ���������չ��ʽ��a�������Ӵ�С���е����ϵ�������磬��a+b��2=a2+2ab+b2չ��ʽ�е�ϵ��1��2��1ǡ�ö�Ӧͼ�е����е����֣����磬��a+b��3=a3+3a2b+3ab2+b3չ��ʽ�е�ϵ��1��3��3��1ǡ�ö�Ӧͼ�е����е����֣�������۲��ͼ��д����a+b��4��չ��ʽ����a+b��4= �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com