
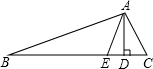
 如图,已知△ABC中,AD是高,AE是角平分线.
如图,已知△ABC中,AD是高,AE是角平分线.分析 (1))根据∠B=20°,∠C=60°,得出∠BAC的度数,再根据AE是角平分线,AD是高,分别得出∠EAC和∠DAC的度数,从而求出答案;
(2)证明过程同(1),只不过把∠B和∠C的度数用字母代替,从而用字母表示出各个角的度数.
解答 解:(1)∵∠B=20°,∠C=60°,
∴∠BAC=180°-20°-60°=100°,
∵AE是角平分线,
∴∠EAC=50°,
∵AD是高,
∴∠ADC=90°,
∴∠DAC=30°,
∴∠EAD=∠EAC-∠DAC=50°-30°=20°;
(2))∵∠B=α,∠C=β,
∴∠BAC=180°-α-β,
∵AE是角平分线,
∴∠EAC=90°-$\frac{1}{2}$α-$\frac{1}{2}$β,
∵AD是高,
∴∠ADC=90°,
∴∠DAC=90°-β,
∴∠EAD=∠EAC-∠DAC=(90°-$\frac{1}{2}$α-$\frac{1}{2}$β)-(90°-β)=$\frac{1}{2}$(β-α).
点评 此题考查了三角形内角和定理和三角形的角平分线、高、中线,解题的关键是根据三角形的内角和是180°,分别求出各个角的度数.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{2}$,则a的值是3+$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{2}$,则a的值是3+$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com