
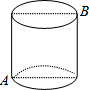
 如图,己知圆柱底面周长为24cm,高为9cm,则蚂蚁在圆柱表面从A点爬到B点的最短路程是15cm.
如图,己知圆柱底面周长为24cm,高为9cm,则蚂蚁在圆柱表面从A点爬到B点的最短路程是15cm.  开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
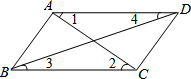 如图所示,下列四组条件中,不能判定AD∥BC的是( )
如图所示,下列四组条件中,不能判定AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠ABC=∠ADC | D. | ∠BAD+∠ABC=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
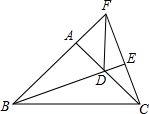 如图,△ABC中,∠BAC=90°,BD是∠ABC的平分线,BD⊥CF交CF于点E,直线CE交BA的延长线于点F且AD=AF.
如图,△ABC中,∠BAC=90°,BD是∠ABC的平分线,BD⊥CF交CF于点E,直线CE交BA的延长线于点F且AD=AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
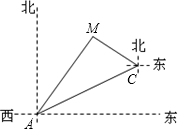 如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)
如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
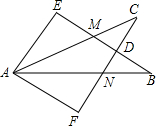 如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com