

���� ��1�����ͼ1��ʾ������A��AG��BC�ڵ�G������Rt��APG�����ù��ɶ������AP�ij��ȣ�
��2�����ͼ2��ʾ�����������ĵ�P����������ֱ�������Σ���������ǵ����Ǻ���ֵ����ǵĶ�����
��3�����жϳ�AP��FQ�������ó�AP��BC���������AP=BP=CP=$\frac{3}{2}$��������ı��ε������ʽ���ɵó����ۣ�
��� �⣺��1�������⻭��ͼ�Σ����ͼ1��ʾ��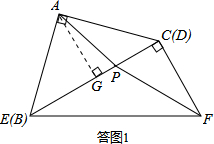
�����⣬�á�CFB=60�㣬FPΪ��ƽ���ߣ����CFP=30�㣬
��CF=BC•tan30��=3��$\frac{\sqrt{3}}{3}$=$\sqrt{3}$��
��CP=CF•tan��CFP=$\sqrt{3}��\frac{\sqrt{3}}{3}$=1��
����A��AG��BC�ڵ�G����AG=$\frac{1}{2}$BC=$\frac{3}{2}$��
��PG=CG-CP=$\frac{3}{2}$-1=$\frac{1}{2}$��
��Rt��APG�У��ɹ��ɶ����ã�
AP=$\sqrt{A{G}^{2}+P{G}^{2}}$=$\frac{\sqrt{10}}{2}$��
��2���ɣ�1����֪��FC=$\sqrt{3}$��
���ͼ2��ʾ���Ե�AΪԲ�ģ���FC=$\sqrt{3}$��Ϊ�뾶��������BC���ڵ�P1��P2����AP1=AP2=$\sqrt{3}$��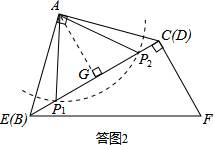
����A��AG��BC�ڵ�G����AG=$\frac{1}{2}$BC=$\frac{3}{2}$��
��Rt��AGP1��cos��P1AG=$\frac{AG}{A{P}_{1}}=\frac{\frac{3}{2}}{\sqrt{3}}$=$\frac{\sqrt{3}}{2}$��
���P1AG=30�㣬
���P1AB=45��-30��=15�㣻
ͬ����ã���P2AG=30�㣬��P2AB=45��+30��=75�㣮
���PAB�Ķ���Ϊ15���75�㣮
��3�����ͼ3��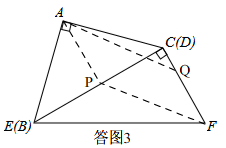
����A��P��F��QΪ�����ƽ���ı��εĶ���Qǡ���ڱ�FC�ϣ�
��AP��QF��
���APC=��BCF��
�ߡ�BCF=90�㣬
���APC=90�㣬
��R��ABC�У���ABC=45�㣬BC=3��
��AC=AB=$\frac{3\sqrt{2}}{2}$��
��AP=BP=CP=$\frac{1}{2}$BC=$\frac{3}{2}$��
��Sƽ���ı���APFQ=AP��PC=$\frac{3}{2}$��$\frac{3}{2}$=$\frac{9}{4}$��
������P�˶���BC�е��λ��ʱ����A��P��F��QΪ�����ƽ���ı��εĶ���Qǡ���ڱ�FC�ϣ��������$\frac{9}{4}$��
���� �������ı����ۺ��⣬��Ҫ�����˽�ƽ���ߵ����壬������Ǻ��������ɶ���������ֱ�������ε����ʣ��Ȿ��Ĺؼ�������ֱ�������ε����ʵ����ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
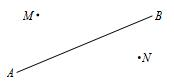 ��ͼ��һ�������ڱ�ֱ�Ĺ�·AB����A��B��ʻ��M��N�ֱ���λ�ڹ�·AB����Ĵ�ׯ������ʻ����Pʱ�����ׯM�����������ʻ����Qʱ�����ׯN�����������ʻ����Oʱ������ׯM��N�ľ���֮����С������ͼ�й�·AB�Ϸֱ���P��Q��O��λ�ã���˵�����ɣ�
��ͼ��һ�������ڱ�ֱ�Ĺ�·AB����A��B��ʻ��M��N�ֱ���λ�ڹ�·AB����Ĵ�ׯ������ʻ����Pʱ�����ׯM�����������ʻ����Qʱ�����ׯN�����������ʻ����Oʱ������ׯM��N�ľ���֮����С������ͼ�й�·AB�Ϸֱ���P��Q��O��λ�ã���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -8��-10 | B�� | -8��10 | C�� | 8��-10 | D�� | 8��10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2-x}$ | B�� | $\sqrt{x-2}$ | C�� | -$\sqrt{2-x}$ | D�� | -$\sqrt{x-2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ӳ�Ĺ�����С���Ӽ�ȥʳ�ó���ͣ�����ȥͼ��ݶ�����Ȼ��ؼң�����x��ʾʱ�䣬y��ʾС����ҵľ��룬С���ҡ�ʳ�á�ͼ�����ͬһֱ���ϣ�����ͼ���ṩ����Ϣ������˵����ȷ���У�������
��ͼ��ӳ�Ĺ�����С���Ӽ�ȥʳ�ó���ͣ�����ȥͼ��ݶ�����Ȼ��ؼң�����x��ʾʱ�䣬y��ʾС����ҵľ��룬С���ҡ�ʳ�á�ͼ�����ͬһֱ���ϣ�����ͼ���ṩ����Ϣ������˵����ȷ���У�������| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2$\sqrt{3}$��2=6 | B�� | $\sqrt{1\frac{25}{49}}$=1$\frac{5}{7}$ | ||
| C�� | $\sqrt{��-121������-9��}$=$\sqrt{121}$��$\sqrt{9}$=33 | D�� | $\sqrt{��-4��^{2}}$=��4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com