方法一:
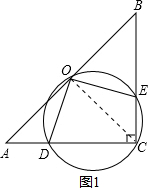
解:(1)连接OC如图:
∵∠ACB=90°,AC=BC,
∴OA=OC,∠A=∠OCE=45°,∠AOC=90°,
又∵∠DOE=180°-∠ACB=90°,
∴∠AOD=90°-∠DOC,∠COE=90°-∠DOC,
∴∠AOD=∠COE,
∴△AOD≌△COE,
∴OD=OE,
(2)∵△AOD≌△COE,
∴S
△AOD=S
△COE,
∴S
四边形ODCE=S
△AOC=

S
△ABC,
∴S
四边形ODCE=

×

×2×2=1;
方法二:
(1)过O分别作OM⊥AC于M,ON⊥BC于N如图
则四边形OMCN是矩形,∠MON=90°
∵OM∥BC,
∴△AOM∽△ABC,
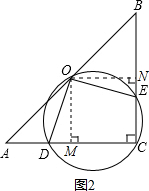
∴
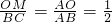
,
又∵BC=2,
∴OM=1,
同理ON=1,
OM=ON,
四边形OMCN是正方形,
∵∠DOM=90°-∠MOE,∠EON=90°-∠MOE,
∴∠DOM=∠EON,
又∵∠OMD=∠ONE=90°,
∴△DOM≌△EON,
∴OD=OE;
(2)∵△DOM≌△EON,
∴S
△ODM=S
△OEN,
∴S
四边形ODCE=S
正方形OMCN,
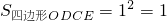
.
分析:(1)首先连接OC,根据等腰直角三角形的性质得出,∠A=∠OCE=45°,进而得出∠AOD=∠COE,即可得出△AOD≌△COE,得出OD=OE;
(2)根据△AOD≌△COE,得出S
△AOD=S
△COE,即可求出S
四边形ODCE=S
△AOC=

S
△ABC,得出答案即可.
点评:此题主要考查了全等三角形的判定以及图形面积求法,根据等腰直角三角形的性质得出∠AOD=∠COE是解题关键.

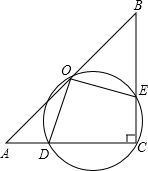 如图,△ABC中,∠ACB=90°,AC=BC=2,O是AB的中点,经过O、C两点的圆分别与AC、BC相交于D、E两点.
如图,△ABC中,∠ACB=90°,AC=BC=2,O是AB的中点,经过O、C两点的圆分别与AC、BC相交于D、E两点. 方法一:
方法一: S△ABC,
S△ABC, ×
× ×2×2=1;
×2×2=1;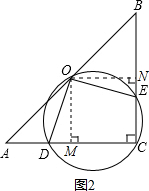
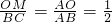 ,
,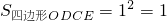 .
. S△ABC,得出答案即可.
S△ABC,得出答案即可.

 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.