
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��B�������ǣ���1��0��������OA=OC=4OB������P�ڹ�A��B��C������������ϣ�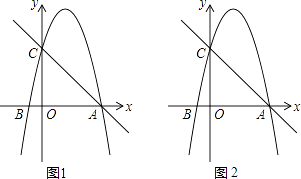
��1���������ߵĽ���ʽ��
��2���Ƿ���ڵ�P��ʹ�á�ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱ��y���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF�ij������ʱ��д����P�����꣨��Ҫ��д������̣���
���𰸡�
��1��
�⣺��B����1��0����֪OB=1��
��OA=OC=4OB��
��OA=OC=4��OB=1��
��C��0��4����A��4��0����
�������ߵĽ���ʽ��y=ax2+bx+c��
��  ��
��
��ã�  ��
��
�������ߵĽ���ʽ��y=��x2+3x+4��
��2��
�⣺���ڣ�
�ٵ���CΪֱ�Ƕ���ʱ��
����C��CP1��AC�����������ڵ�P1��
����P1��y��Ĵ��ߣ�������M��M����ͼ1��
�ߡ�A CP1=90�㣬���MCP1+��ACO=90�㣮
�ߡ�ACO+��OAC=90�㣬
���MCP1=��OAC��
��OA=OC��
���MCP1=��OAC=45�㣬
���MCP1=��MP1C��
��MC=MP1��
��P��m����m2+3m+4����
��m=��m2+3m+4��4��
��ã�m1=0����ȥ����m2=2��
��m=2��
��ʱ��m2+3m+4=6��
��P1P�������ǣ�2��6����
�ڵ���AΪֱ�Ƕ���ʱ��
��A��AP2��AC���������ڵ�P2��
����P2��y��Ĵ��ߣ�������N��AP��y���ڵ�F����ͼ2��
��P2N��x�ᣬ
�ɡ�CAO=45��á�OAP2 =45�㣬
���FP2N=45�㣬AO=OF��
��P2N=NF��
��P2��n����n2+3n+4����
��n+4=������n2+3n+4����
��ã�n1=��2��n2=4����ȥ����
��n=��2��
��ʱ��n2+3n+4=��6��
��P2�������ǣ���2����6����
����������P�������ǣ�2��6����2����6����


��3��
�⣺��EF���ʱ����P�������ǣ� ![]() ��2����
��2���� ![]() ��2����
��2����
����������£�
����OD���������֪���ı���OFDE�Ǿ��Σ���OD=EF��
���ݴ��߶���̿ɵã���OD��ACʱ��OD����EF����̣�
�ɣ�1����֪����ֱ�ǡ�AOC�У�OC=OA=4��
���ݵ��������ε����ʿɵã�D��AC���е㣮
�֡�DF��OC��
���AFD�ס�AOC��
�� ![]() =
= ![]() =
= ![]()
��DF= ![]() OC=2��
OC=2��
���D����������2��
���P��������Ҳ��2��
�⩁x2+3x+4=2�ã�
x1= ![]() ��x2=
��x2= ![]() ��
��
���P�������� ![]() ��2����
��2���� ![]() ��2����
��2����
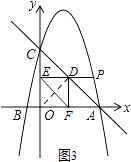
����������1��ֻ�����A��B��C��������꣬Ȼ�����ô���ϵ�����Ϳ���������ߵĽ���ʽ����2���ɷ��������������CΪֱ�Ƕ��㣬����AΪֱ�Ƕ��㣩���ۣ�Ȼ����ݵ�P���ݡ�������֮��Ĺ�ϵ����������ϵ���Ϳ������P�����ꣻ��3������OD �� ���ı���OFDE�Ǿ��Σ���OD=EF �� ���ݴ��߶���̿ɵõ�OD��ACʱ��OD����EF����̣�Ȼ��ֻ�������D�������꣬�Ϳɵõ���P�������꣬�Ϳ������P�����꣮
�����㾫����������Ҫ��������������������Ľ�������֪ʶ�㣬��Ҫ����һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�͡�CEF���������ȵĵȱ������Σ�����һ����������C������AF��BE���߶�AF��BE�������Ĵ�С��ϵ��֤����IJ��룮 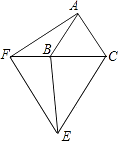
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��ABC��ƽ���߽�AC�ڵ�E������E��BE�Ĵ��߽�AB�ڵ�F����O�ǡ�BEF�����Բ�� 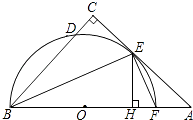
��1����֤��AC�ǡ�O�����ߣ�
��2������E��EH��AB�ڵ�H����֤��CD=HF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BCΪֱ����Բ����ABC������AB��AC�ڵ�D��E����EǡΪAC���е㣬BFΪ��ABC�����ƽ���ߣ���F��Բ�ϣ��������һ���̶ȵ�ֱ�ߣ�����A��һ���߶Σ�����ABC�ֳ������ȵ������֣� 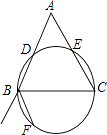
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A����4��0.5����B����1��2����һ�κ���y=ax+b�뷴�������� ![]() ��m��0��ͼ����������㣬AC��x����C��BD��y����D��
��m��0��ͼ����������㣬AC��x����C��BD��y����D��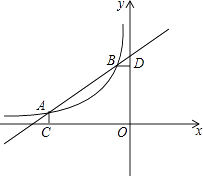
��1������ͼ��ֱ�ӻش��ڵڶ������ڣ���xȡ��ֵʱ��һ�κ������ڷ�����������ֵ��
��2����һ�κ�������ʽ��m��ֵ��
��3��P���߶�AB�ϵ�һ�㣬����PC��PD������PCA�͡�PDB�����ȣ����P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�г�Ӫ������Ӫ��Ա�ĸ���������y(Ԫ)���Ӫ��Աÿ�µ�������x(���)��һ�κ�����ϵ����ͼ����ͼ11��ʾ������ͼ���ṩ����Ϣ������������⣺
(1)���Ӫ��Ա�ĸ���������y(Ԫ)���Ӫ��Աÿ�µ�������x(���)(x��0)֮��ĺ�����ϵʽ��
(2)��֪�ù�˾Ӫ��Ա��ƽ5�·ݵ�������Ϊ1.2���������ƽ5�·ݵ����룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�������ADE�Ķ���A�غϣ�AD=AE����DAE=30�㣬����ADE�ƶ���A��ת������ת�����У���BD=CEʱ����BAD�Ĵ�С������ �� 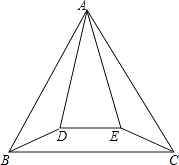
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABFG��������CDEF�Ķ����ڱ߳�Ϊ1������������ĸ���ϣ�
(1)����ƽ��ֱ������ϵ��ʹ��B��C������ֱ�Ϊ(0��0)��(5��0)����д����A��D��E��F��G�����ꣻ
(2)����BE��CG�ཻ�ڵ�H��BE��CG����𣿲������BHC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ף��ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�������B��������߽�x���ڵ�A��D����y���ڵ�E������AB��AE��BE����֪tan��CBE= ![]() ��A��3��0����D����1��0����E��0��3����
��A��3��0����D����1��0����E��0��3����
��1���������ߵĽ���ʽ������B�����ꣻ
��2����֤��CB�ǡ�ABE���Բ�����ߣ�
��3����̽�����������Ƿ����һ��P��ʹ��D��E��PΪ��������������ABE���ƣ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��4�����AOE��x��������ƽ��t����λ���ȣ�0��t��3��ʱ����AOE���ABE�ص����ֵ����Ϊs����s��t֮��ĺ�����ϵʽ����ָ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com