
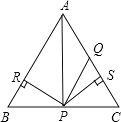
【题目】如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论①点P在∠A的平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中正确的是( )
A. ①② B. ①②④ C. ①②③ D. ①②③④
【答案】D
【解析】
因为△ABC为等边三角形,根据已知条件可推出Rt△ARP≌Rt△ASP,则AR=AS,故(2)正确,∠BAP=∠CAP,所以AP是等边三角形的顶角的平分线,故(1)正确,根据等腰三角形的三线合一的性质知,AP也是BC边上的高和中线,即点P是BC的中点,因为AQ=PQ,所以点Q是AC的中点,所以PQ是边AB对的中位线,有PQ∥AB,故(3)正确,又可推出△BRP≌△QSP,故(4)正确.
∵PR⊥AB于R,PS⊥AC于S,
∴∠ARP=∠ASP=90°,
∵PR=PS,AP=AP,
∴Rt△ARP≌Rt△ASP,
∴AR=AS,故(2)正确,∠BAP=∠CAP,
∴AP是等边三角形的顶角的平分线,故(1)正确;
∴AP是BC边上的高和中线,即点P是BC的中点,
∵AQ=PQ,
∴点Q是AC的中点,
∴PQ是边AB对的中位线,
∴PQ∥AB,故(3)正确;
∵∠B=∠C=60°,∠BRP=∠CSP=90°,BP=CP,
∴△BRP≌△QSP,故(4)正确,
∴全部正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.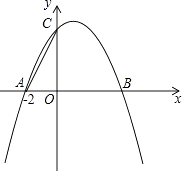
(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的对话:
MM:“请帮我称些梨.”
售货员:“您上次买的梨卖没了,您试一试新进的苹果,价格虽然比梨贵些,但苹果营养价
值更高.”
MM:“好,我跟上次一样,也买30元钱.”
对比两次的电脑小票,MM发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5
千克.
根据上面的对话和MM发现,分别求出苹果和梨的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(-4,1),B(-3,3),C(-1,2).

(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小.(不写作法,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠C=90°,∠BAC=30°,点 D 是 BC 边上的点,AB=18,将△ABC 沿直线 AD 翻折,使点 C 落在 AB 边上的点 E 处,若点 P 是直线 AD 上的动点,则 BP+EP 的最小值是____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com