练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一次函数片与的图象如图所示，下列说法：

    ①ab＜0；　

    ②函数y＝ax+d不经过第一象限；

    ③函数y＝cx+b中，y随x的增大而增大；

    ④3a+b＝3c+d

    其中正确的个数有（）

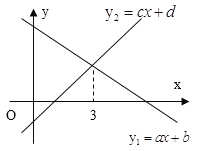
    A.4个B.3个C.2个D.1个

    【答案】A

    【解析】

    仔细观察图象：①a的正负看函数y1=ax+b图象从左向右成何趋势，b的正负看函数y1=ax+b图象与y轴交点即可；

    ②观察函数图象可以直接得到答案；

    ③观察函数图象可以直接得到答案；

    ④根据两直线交点可以得到答案．

    由图象可得：a＜0，b＞0，c＞0，d＜0，

    ∴ab＜0，故①正确；

    函数y=ax+d的图象经过第二，三，四象限，即不经过第一象限，故②正确，

    函数y=cx+b中，y随x的增大而增大，故③正确；

    ∵一次函数y1=ax+b与y2=cx+d的图象的交点的横坐标为3，

    ∴3a+b=3c+d，故④正确．

    综上所述，正确的结论有4个．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

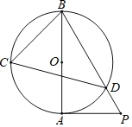
    【题目】如图AB是⊙O的直径，PA与⊙O相切于点A，BP与⊙O相交于点D，C为⊙O上的一点，分别连接CB、CD，∠BCD＝60°．

    (1)求∠ABD的度数；

    (2)若AB＝6，求PD的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展“传统文化”知识竞赛，已知该校七年级男生和女生各有学生200人，从中各随机抽取20名学生进行抽样调查，获得了他们知识竞赛成绩（满分100分），并进行整理，得到下面部分信息．

    男生：74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74

    女生：76 87 93 65 78 94 89 68 95 54 89 87 89 89 77 94 86 87 92 91

    成绩

    50≤x≤59

    60≤x≤69

    70≤x≤79

    80≤x≤89

    90≤x≤100

    男生

    0

    1

    10

    1

    8

    女生

    1

    2

    a

    8

    6

    平均数、中位数、众数、方差如表所示：

    成绩

    平均数

    中位数

    众数

    方差

    男生

    84

    77

    74

    145.4

    女生

    84

    b

    89

    115.6

    根据以上信息，回答下列问题：

    （1）a＝　 　，b＝　 　；

    （2）你认为七年级学生中，男生还是女生的总体成绩较好，为什么？（至少从两个不同的角度说明）

    （3）若在此次竞赛中，该校七年级学生中有四人取得100分的好成绩，且恰好是两个男生两个女生．现从这四人中随机抽取两人参加市里的竞赛，求这两人恰好是一男一女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了弘扬传统文化，某校组织八年级全体学生参加“恰同学少年，品诗词美韵”的古诗词比赛．比赛结束后，学校随机抽取的部分学生成绩作为样本，并进行整理后分成下面5组，分的小组称为“诗词少年”组，分的小组称为“诗词居士”组，分的小组称为“诗词圣手”组，分的小组称为“诗词达人”组，分的小组称为“诗词泰斗”组；下面是将整理的样本绘制的不完整的频数分布直方图，请结合提供的信息解答下列问题：

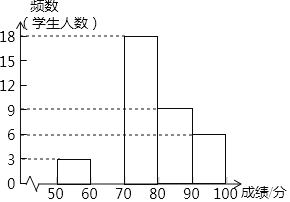
    (1)若“诗词泰斗”组成绩的频率12.5%，求出样本容量，补全频数分布直方图；

    (2)以各组组中值代表本组的选手的平均成绩，计算样本中不含“诗词圣手”组的其他四组学生的平均成绩；

    (3)学校决定对成绩进人“诗词圣手”、“诗词达人”、“诗词泰斗“组的学生进行奖励，若八年级共有240名学生，请通过计算推断，大约有多少名学生获奖．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】垃圾分类问题受到全社会的广泛关注，我区某校学生会向全校2100名学生发起了“垃圾要回家，请你帮助它”的捐款活动，用于购买垃圾分类桶．为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如图统计图1和图2，请根据相关信息，解答下列问题：

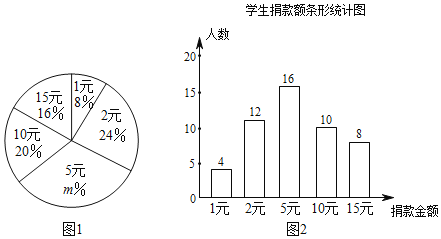
    （1）本次接受随机抽样调查的学生人数为　 ，图1中m的值是　 ；

    （2）求本次调查获取的样本数据的平均数、众数和中位数；

    （3）根据样本数据，估计该校本次活动捐款金额为5元的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知顶点为D的抛物线与x轴交于A(－1，0)，C(3，0)两点，与y轴交于B点．

    (1)求该抛物线的解析式及点D坐标；

    (2)若点Q是该抛物线的对称轴上的一个动点，当AQ＋QB最小时，直接写出直线AQ的函数解析式；

    (3)若点P为抛物上的一个动点，且点P在x轴上方，过P作PK垂直x轴于点K，是否存在点P使得A,K,P三点形成的三角形与△DBC相似?如存在，求出点P的坐标，如不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；

    （2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．

    （3）运用（1）（2）解答中所积累的经验和知识，完成下题：

    如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE="10," 求直角梯形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线AB与函数y＝（x＞0）的图象交于点A（m，2），B（2，n）．过点A作AC平行于x轴交y轴于点C，在y轴负半轴上取一点D，使OD＝OC，且△ACD的面积是6，连接BC．

    （1）求m，k，n的值；

    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

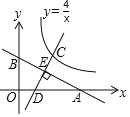
    【题目】如图，直线y＝﹣x+2分别与x轴，y轴交于点A，B，点C是反比例函数y＝的图象在第一象限内一动点．过点C作直线CD⊥AB．交x轴于点D，交AB于点E．则CE：DE的最小值为_____．

    查看答案和解析>>

    同步练习册答案