
【题目】如图,直线y=﹣![]() x+2分别与x轴,y轴交于点A,B,点C是反比例函数y=
x+2分别与x轴,y轴交于点A,B,点C是反比例函数y=![]() 的图象在第一象限内一动点.过点C作直线CD⊥AB.交x轴于点D,交AB于点E.则CE:DE的最小值为_____.
的图象在第一象限内一动点.过点C作直线CD⊥AB.交x轴于点D,交AB于点E.则CE:DE的最小值为_____.
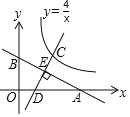
【答案】![]()
【解析】
连接AC,根据题意得到A、B的坐标,以及△ADE∽△ABO,即可求得![]() =
=![]() =
=![]() ,进一步求得
,进一步求得![]() =
=![]() =2tan∠CAE,当∠CAE最小,即AC与双曲线
=2tan∠CAE,当∠CAE最小,即AC与双曲线![]() (x>0)只有一个交点时,
(x>0)只有一个交点时,![]() 最小,设AC的解析式为y=kx﹣4k,则
最小,设AC的解析式为y=kx﹣4k,则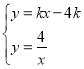 ,消去y整理得到kx2﹣4kx﹣4=0,当AC与双曲线
,消去y整理得到kx2﹣4kx﹣4=0,当AC与双曲线![]() (x>0)只有一个交点时,△=16k2+16k=0,解得k的值,即可求得AC的解析式,进而求得C,D、E的坐标,然后根据平行线分线段成比例求得CE:DE的最小值为
(x>0)只有一个交点时,△=16k2+16k=0,解得k的值,即可求得AC的解析式,进而求得C,D、E的坐标,然后根据平行线分线段成比例求得CE:DE的最小值为![]() .
.
解:如图,连接AC,
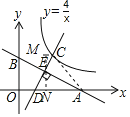
∵直线y=﹣![]() x+2分别与x轴,y轴交于点A,B,
x+2分别与x轴,y轴交于点A,B,
∴A(4,0),B(0,2),
∵CD⊥AB,
∴∠AED=∠AOB=90°,
∵∠DAE=∠BAO,
∴△ADE∽△ABO,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =2tan∠CAE,
=2tan∠CAE,
∴当∠CAE最小,即AC与双曲线![]() (x>0)只有一个交点时,
(x>0)只有一个交点时,![]() 最小,
最小,
设AC的解析式为y=kx﹣4k,则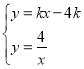 ,消去y整理得:kx2﹣4kx﹣4=0,
,消去y整理得:kx2﹣4kx﹣4=0,
当AC与双曲线![]() (x>0)只有一个交点时,△=16k2+16k=0,解得k=﹣1或k=0(舍去),
(x>0)只有一个交点时,△=16k2+16k=0,解得k=﹣1或k=0(舍去),
∴AC的解析式为y=﹣x+4,
解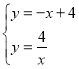 得
得![]() ,
,
∴C(2,2),
设CD的解析式为y=2x+n,则2=4+n,
解得n=﹣2,
∴CD的解析式为y=2x﹣2,
∴D(1,0),
解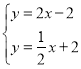 得
得![]() ,
,
∴E(![]() ,
,![]() ),
),
过E点作MN⊥x轴于N,交过C点与x轴平行的直线于M,
∴MC∥DN,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】一次函数片![]() 与
与![]() 的图象如图所示,下列说法:
的图象如图所示,下列说法:
①ab<0;
②函数y=ax+d不经过第一象限;
③函数y=cx+b中,y随x的增大而增大;
④3a+b=3c+d
其中正确的个数有()
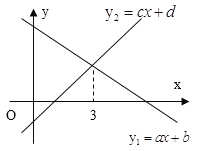
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
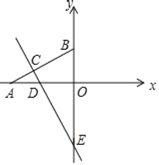
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC交线段AB于点C,交x轴于点D.若C点坐标为(-6.m),求:直线AB的表达式和经过点C得反比例函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市某公司自主设计了一款可控温杯,每个生产成本为16元,投放市场进行了试销.经过调查得到每月销售量y(万个)与销售单价x(元/个)之间关系是一次函数的关系,部分数据如下:
销售单价x(元/个) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万个) | … | 60 | 50 | 40 | 30 | … |
(1)求y与x之间的函数关系;
(2)该公司既要获得一定利润,又要符合相关部门规定(一件产品的利润率不得高于50%)请你帮助分析,公司销售单价定为多少时可获利最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
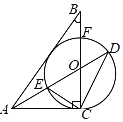
【题目】如图,在△ABC中,∠ACB=90°,AO平分∠BAC,交BC于点O.以O为圆心,OC为半径作⊙O,分别交AO,BC于点E,F.
(1)求证:AB是⊙O的切线;
(2)延长AO交⊙O于点D,连接CD,若AD=2AC,求tanD的值;
(3)在(2)的条件下,设⊙O的半径为3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广劳动教育,美化校园环境,学校决定在农场基地铺设一条观景小道.经设计,铺设这条小道需A,B两种型号石砖共200块.已知:购买3块A型石砖,2块B型石砖需要110元;购买5块A型石砖,4块B型石砖需要200元.
(1)求A,B两种型号石砖单价各为多少元?
(2)已知B型石砖正在进行促销活动:购买B型石砖数量在60块以内(包括60块)时,不优惠;购买B型石砖数量超过60块时,每超过1块,购买的所有B型石砖单价均降0.05元,问:学校采购石砖,最多需要多少预算经费?
查看答案和解析>>
科目:初中数学 来源: 题型:
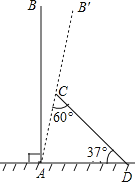
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解家长和学生参与“全国中小学生新冠肺炎疫情防控”专题教育的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;C.仅家长参与;D.家长和学生都未参与.请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了______名学生;
(2)C类所对应扇形的圆心角的度数是_______,并补全条形统计图;
(3)根据抽样调查结果,试估计该校1800名学生中“家长和学生都未参与”的人数.
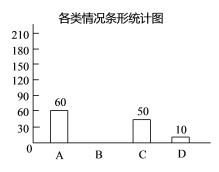

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)交x轴于A,B两点(A在B的左侧),交y轴于点C,抛物线的顶点为P,过点B作BC的垂线交抛物线于点D.
(1)若点P的坐标为(-4,-1),点C的坐标为(0,3),求抛物线的表达式;
(2)在(1)的条件下,求点A到直线BD的距离;
(3)连接DC,若点P的坐标为(-![]() ,-
,-![]() ),DC∥x轴,则在x轴上方的抛物线上是否存在点M,使∠AMB=∠BDC?若存在,求出点M的坐标;若不存在,请说明理由.
),DC∥x轴,则在x轴上方的抛物线上是否存在点M,使∠AMB=∠BDC?若存在,求出点M的坐标;若不存在,请说明理由.
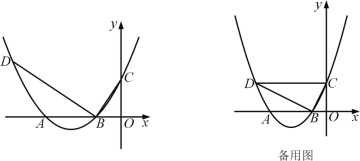
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com