
����Ŀ��Ϊ�ƹ��Ͷ�����������У������ѧУ������ũ����������һ���۾�С��������ƣ���������С����A��B�����ͺ�ʯש��200�飮��֪������3��A��ʯש��2��B��ʯש��Ҫ110Ԫ������5��A��ʯש��4��B��ʯש��Ҫ200Ԫ��
��1����A��B�����ͺ�ʯש���۸�Ϊ����Ԫ��
��2����֪B��ʯש���ڽ��д����������B��ʯש������60�����ڣ�����60�飩ʱ�����Żݣ�����B��ʯש��������60��ʱ��ÿ����1�飬���������B��ʯש���۾���0.05Ԫ���ʣ�ѧУ�ɹ�ʯש�������Ҫ����Ԥ�㾭�ѣ�
���𰸡���1��A��B�����ͺ�ʯש���۷ֱ�Ϊ20Ԫ��25Ԫ����2��ѧУ�ɹ�ʯש�������Ҫ4320ԪԤ�㾭��
��������
��1����A��B�����ͺ�ʯש���۷ֱ�ΪxԪ��yԪ������������3��A��ʯש��2��B��ʯש��Ҫ110Ԫ������3��A��ʯש��4��B��ʯש��Ҫ200Ԫ���з������ü��ɣ�
��2���蹺��B��ʯשm�飬�ɹ�ʯ�������ΪWԪ�����m�ķ�Χ�ó�W��m�Ĺ�ϵʽ������һ�κ��������ʽ�ɣ�
�⣺��1����A��B�����ͺ�ʯש���۷ֱ�ΪxԪ��yԪ��
![]()
���![]()
��A��B�����ͺ�ʯש���۷ֱ�Ϊ20Ԫ��25Ԫ��
��2���蹺��B��ʯשm�飬�ɹ�ʯ�������ΪWԪ��
��0��m��60ʱ��W��20��200��m��+25m��5m+4000��
��֪����m��60ʱ��W�����4300Ԫ��
��60��m��200ʱ��
W��20��200��m��+m[25��0.05��m��60��]����0.05m2+8m+4000����0.05��m��80��2+4320��
��֪����m��80ʱ��W�����4320Ԫ��
��ѧУ�ɹ�ʯש�������Ҫ4320ԪԤ�㾭�ѣ�


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ΪD��������![]() ��x�ύ��A(��1��0)��C(3��0)���㣬��y�ύ��B�㣮
��x�ύ��A(��1��0)��C(3��0)���㣬��y�ύ��B�㣮
(1)��������ߵĽ���ʽ����D���ꣻ
(2)����Q�Ǹ������ߵĶԳ����ϵ�һ�����㣬��AQ��QB��Сʱ��ֱ��д��ֱ��AQ�ĺ�������ʽ��
(3)����PΪ�����ϵ�һ�����㣬�ҵ�P��x���Ϸ�����P��PK��ֱx���ڵ�K���Ƿ���ڵ�Pʹ��A,K,P�����γɵ�����������DBC����?����ڣ������P�����꣬�粻���ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
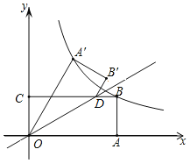
����Ŀ����ͼ������OABC�ı�OA��OC�ֱ���x�ᡢy���ϣ���B�ڵ�һ���ޣ���D�ڱ�BC�ϣ��ҡ�AOD��30�����ı���OA��B��D���ı���OABD����ֱ��OD�Գƣ���A����A��B����B�ֱ��Ӧ������AB��1������������y��![]() ��k��0����ͼ��ǡ�þ�����A����B����k��ֵΪ______��
��k��0����ͼ��ǡ�þ�����A����B����k��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
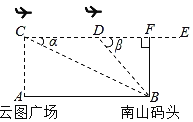
����Ŀ����¡���dzɶ��츮������������̬�̵ع��̣���һ�λ����ۺ�ʵ����У�С��ͬѧ���ڵ���ȤС�������˻����IJ�����ͼ�㳡A����ɽ��ͷB��ֱ�߾��룮�������˻����ƾ������ޣ�Ϊ�˰�ȫ������ֱ�Ӳ��������Dz������·�������ͼ��С������ͼ�㳡A�����Ϸ���C�������ɽ��ͷB�ĸ�������17.09�����������˻�����ɽ��ͷB����ˮƽ����0.9ǧ�����D������ô�ʱ��ɽ��ͷB�ĸ�������45������֪AC��AB��CD��AB������ݲ������ݼ���A��B���صľ��룮�������ȷ��0.1km���ο����ݣ�sin����0.29��tan����0.31��sin�¡�0.71��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
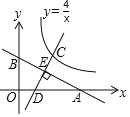
����Ŀ����ͼ��ֱ��y����![]() x+2�ֱ���x�ᣬy�ύ�ڵ�A��B����C�Ƿ���������y��
x+2�ֱ���x�ᣬy�ύ�ڵ�A��B����C�Ƿ���������y��![]() ��ͼ���ڵ�һ������һ���㣮����C��ֱ��CD��AB����x���ڵ�D����AB�ڵ�E����CE��DE����СֵΪ_____��
��ͼ���ڵ�һ������һ���㣮����C��ֱ��CD��AB����x���ڵ�D����AB�ڵ�E����CE��DE����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ��������θ߷�ĵ�����ij���μ���Ʒ�̵��������A��B���ּ���Ʒ��������A�ּ���Ʒ7����B�ּ���Ʒ4������Ҫ760Ԫ��������A�ּ���Ʒ5����B�ּ���Ʒ8������Ҫ800Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2�������̵�������������ּ���Ʒ��100���������г�������ʽ���ת����100������Ʒ���ʽ�����7000Ԫ����������7200Ԫ����ô���̵깲�м��ֽ���������
��3��������A�ּ���Ʒÿ���ɻ�����30Ԫ��B�ּ���Ʒÿ���ɻ�����20Ԫ���ã�2���еĽ�����������һ�ַ����ɻ��������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�꣬ijƶ�����ļ�ͥ���˾�������Ϊ2500Ԫ��ͨ��������ҵ���֣���չ����ֳҵ��2018�꣬��ͥ���˾�������ﵽ��3600Ԫ��
��1�����ƶ����2016�굽2018���ͥ���˾����������ƽ�������ʣ�
��2������ƽ�������ʱ��ֲ��䣬2019���ƶ�����ļ�ͥ���˾��������Ƿ��ܴﵽ4200Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
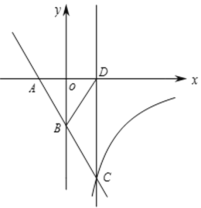
����Ŀ����ֱ֪�ߣ�y1��![]() ��x�ᡢy���ཻ��A��B���㣬��˫����
��x�ᡢy���ཻ��A��B���㣬��˫����![]() (k��0��x��0)�ཻ�ڵ������ĵ�C������C��ֱ��l��x�ᣬ����ΪD������ABD�����Ϊ
(k��0��x��0)�ཻ�ڵ������ĵ�C������C��ֱ��l��x�ᣬ����ΪD������ABD�����Ϊ![]() ����B��AC���е㣮
����B��AC���е㣮
(1)��k��ֵ��
(2)ֱ��д��![]() �Ľ⼯��
�Ľ⼯��
(3)��PΪֱ��l��һ���㣬��P��������Ϊm����APB��30������m�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��������ABCD�Ķ���B��C�������AD�����ڵ�E����AE��1��ED��5�����O�İ뾶Ϊ�� ��
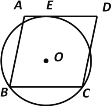
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com