
����Ŀ����ͼ��������y��ax2��bx��c��a��0����x����A��B���㣨A��B����ࣩ����y���ڵ�C�������ߵĶ���ΪP������B��BC�Ĵ��߽��������ڵ�D��
��1������P������Ϊ����4����1������C������Ϊ��0��3�����������ߵı���ʽ��
��2���ڣ�1���������£����A��ֱ��BD�ľ��룻
��3������DC������P����������![]() ����
����![]() ����DC��x�ᣬ����x���Ϸ������������Ƿ���ڵ�M��ʹ��AMB����BDC�������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
����DC��x�ᣬ����x���Ϸ������������Ƿ���ڵ�M��ʹ��AMB����BDC�������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
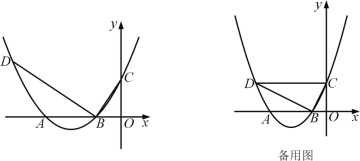
���𰸡���1��y��![]() x 2��2x��3����2����A��ֱ��BD�ľ���Ϊ
x 2��2x��3����2����A��ֱ��BD�ľ���Ϊ![]() ����3�����ڣ�M1��
����3�����ڣ�M1��![]() ��4����M2��
��4����M2��![]() ��4��
��4��
��������
��1�����ô���ϵ������C��0��3�����뼴�ɽ�����⣻
��2�������A��B��C�������ꡣ�̶����AB��BC�߶γ�������AF��BD��F���ɵ���ABF����BCO������sin��ABF��sin��BCO������⣻
��3����DH��x����H����A��x1��0����B��x2��0��������DBH�ס�BCO�ɵ�![]() ��
�� ![]() ����ϵ����ϵ����ϵ�ɵ�c 2��x1x2��c��
����ϵ����ϵ����ϵ�ɵ�c 2��x1x2��c�� ![]() ���̶��ִ���ϵ�����������ʽΪy��
���̶��ִ���ϵ�����������ʽΪy�� ![]() x 2��
x 2��![]() x��2���ɵ�ABC�������꣬���ɾ���A��B��M�����Բ��Բ��ΪQ�����Q���꣬�̶���
x��2���ɵ�ABC�������꣬���ɾ���A��B��M�����Բ��Բ��ΪQ�����Q���꣬�̶���
QM=QA������⣮
�⣺��1���������ߵĽ���ʽΪy��a( x��4 )2��1��
��C��0��3�����룬��3��a( 0��4 )2��1��a�� ![]() ��
��
�������ߵĽ���ʽΪy�� ![]() ( x��4 )2��1����y��
( x��4 )2��1����y��![]() x 2��2x��3��
x 2��2x��3��
��2���� ![]() x 2��2x��3��0�����x1����2��x2����6��
x 2��2x��3��0�����x1����2��x2����6��
��A����6��0����B����2��0����
��OA��6��OB��2��AB��4��
��x��0����y��3����C��0��3����
��OC��3��
��BC��![]() ��
��![]() ��
��![]() ��
��
��AF��BD��F��
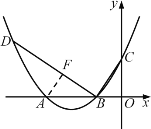
��DB��BC�����DBC��90�������ABF����CBO��90��
�ߡ�BCO����CBO��90����
���ABF����BCO
��![]() ��sin��ABF��sin��BCO��
��sin��ABF��sin��BCO�� ![]() ��
�� ![]()
��AF�� ![]() AB��
AB��![]() ��
��![]() ������A��ֱ��BD�ľ���Ϊ
������A��ֱ��BD�ľ���Ϊ![]() ��
��
��3����DH��x����H
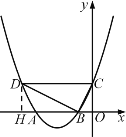
��A��x1��0����B��x2��0��
�������ߵĶԳ��Կ�֪AH��BO
��BH��OH��OB��OH��AH��OA����x1
��DC��x�ᣬ��DH��CO��c
��DB��BC�����DBH�ס�BCO
��![]() ��
�� ![]() ����
����![]() ��
�� ![]() ����c 2��x1x2
����c 2��x1x2
��ax 2��bx��c��0����x1x2��![]() ����c 2��
����c 2�� ![]() ����c��
����c�� ![]()
��P����![]() ����
����![]() �������������ߵĽ���ʽΪy��a( x��
�������������ߵĽ���ʽΪy��a( x�� ![]() )2��
)2�� ![]()
��x��0����c�� ![]() a��
a��![]() ��
��
��![]() a��
a��![]() ��
��
���a����![]() ����ȥ����a��
����ȥ����a�� ![]()
�������ߵĽ���ʽΪy�� ![]() ( x��
( x�� ![]() )2��
)2��![]() ����y��
����y�� ![]() x 2��
x 2��![]() x��2
x��2
��A����4��0����B����1��0����C��0��2��
AB��3��OB��1��OC��2
�辭��A��B��M�����Բ��Բ��ΪQ������QA��QB��QM
��QN��AB��N
��AN��BN�� ![]() ��QA��QB��QM����AQN����AMB����BDC
��QA��QB��QM����AQN����AMB����BDC
��DC��x�ᣬ���BDC����ABD����BCO
���AQN����BCO��
��![]() ��tan��AQN��tan��BCO��
��tan��AQN��tan��BCO�� ![]() ��
�� ![]()
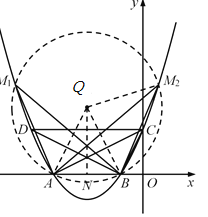
��QN��2AN��AB��3����Q���� ![]() ��3����QA 2��
��3����QA 2�� ![]()
��M��m��y��������y�� ![]() m 2��
m 2�� ![]() m��2
m��2
��QM 2��( m�� ![]() )2��( y��3 )2
)2��( y��3 )2
��( m�� ![]() )2��( y��3 )2��
)2��( y��3 )2�� ![]()
m 2��5m��4��y 2��6y��0��2y��y 2��6y��0
y 2��4y��0�����y��0����ȥ����y��4
�� ![]() x 2��
x 2�� ![]() x��2��4�����x��
x��2��4�����x�� ![]()
��M1��![]() ��4����M2��
��4����M2��![]() ��4��
��4��


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
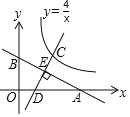
����Ŀ����ͼ��ֱ��y����![]() x+2�ֱ���x�ᣬy�ύ�ڵ�A��B����C�Ƿ���������y��
x+2�ֱ���x�ᣬy�ύ�ڵ�A��B����C�Ƿ���������y��![]() ��ͼ���ڵ�һ������һ���㣮����C��ֱ��CD��AB����x���ڵ�D����AB�ڵ�E����CE��DE����СֵΪ_____��
��ͼ���ڵ�һ������һ���㣮����C��ֱ��CD��AB����x���ڵ�D����AB�ڵ�E����CE��DE����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣬Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵġ�������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ�(�ɼ�xȡ�������ܷ�100��)��Ϊ���������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.05 |
��60��x��70 | 30 | 0.15 |
��70��x��80 | 40 | n |
��80��x��90 | m | 0.35 |
��90��x��100 | 50 | 0.25 |
�����������Ϣ������������⣺
(1)m���� ����n���� ����
(2)�벹ȫƵ���ֲ�ֱ��ͼ��
(3)���ɼ���90������(����90��)��Ϊ���š��ȣ����У�μ���α�����3000��ѧ���гɼ����š���Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����IΪ��ABC�����ģ�AB=4��AC=3��BC=2������ACBƽ��ʹ�䶥����I�غϣ���ͼ����Ӱ���ֵ��ܳ�Ϊ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵxOy�У����κ���y=mx 2 +2mx��4��m��0����ͼ����x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C����ABC�����Ϊ12��
��1����������κ����Ľ���ʽ��
��2����D������Ϊ����2��1������P�ڶ��κ�����ͼ���ϣ���ADPΪ��ǣ���tan��ADP=2�������P�ĺ����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
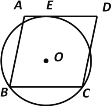
����Ŀ����ͼ����O��������ABCD�Ķ���B��C�������AD�����ڵ�E����AE��1��ED��5�����O�İ뾶Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺ÿ���ڽǶ���ȵİ˱��ν����Ƚǰ˱��Σ�����֪�����Ƚǰ˱��ε��ڽǶ�����135�������棬�������о�����һЩ�������ж���
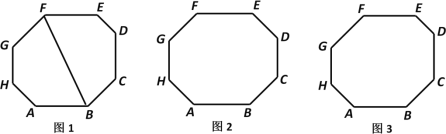
��1����ͼ1���Ƚǰ˱���ABCDEFGH�У�����BF��
����ֱ��д����ABF����GFB�Ķ�����
����֤��AB��EF��
�����ǰ�AB��EF��Ϊ�˱��ε�һ�����Աߣ��ɢ�ͬ���ɵã�BC��FG��CD��GH��DE��HA���������Ա�Ҳ�ֱ�ƽ�У���ģ��ƽ���ı������ʵ�ѧϰ���飬��һ�仰�����Ƚǰ˱��ε���һ���ʣ�
��2����ͼ2���Ƚǰ˱���ABCDEFGH�У������AB��EF��BC��FG���������������Ա�CD��GH��DE��HA�ֱ������֤����Ľ��ۣ�
��3����ͼ3���˱���ABCDEFGH�У����������Ա߷ֱ�ƽ�У�����Ȼ�С�A����E����B����F����C����G����D����H����̽�����ð˱���������Ҫ��֪�����ڽ�Ϊ135�������ܱ�֤��һ���ǵȽǰ˱��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
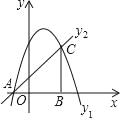
����Ŀ����ͼ��������y1��a��x��1��2+4��x�ύ��A����1��0����
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2��һ�κ���y2��x+1��ͼ�����������ཻ��A��C���㣬����C��CB��ֱ��x���ڵ�B�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͣ�β�ͣѧ��ѧϰ����������ij��ͨ��������Դ��������ƽ̨�����ߵ���Ϊȫ����Сѧ�������������п�������Ϊ�˽�ѧ��ÿ���ѧϰʱ���������ȫ�������ȡ�˲��ֳ���ѧ�������ʾ����飬�ֽ����������Ƴ����²�������ͳ��ͼ���������ͼ���е���Ϣ����������⣺
��� | ѧϰʱ��x��h�� | �������ˣ� |
A | 2.5��x��3 | 40 |
B | 3��x��3.5 | 170 |
C | 3.5��x��4 | 350 |
D | 4��x��4.5 | |
E | 4.5��x��5 | 90 |
F | 5Сʱ���� | 50 |
��1
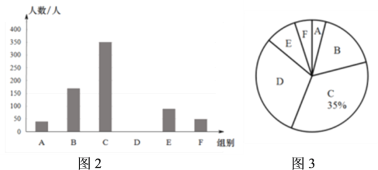
��1����β����ʾ�����ij���ѧ���� �ˣ���λ������ �飮
��2��ͼ3��D���Ӧ�ĽǶ����� �� ������ȫͼ2 ����ͳ��ͼ��
��3����ij���г���ѧ��2.8���ˣ������ÿ����������п�����ѧϰʱ��3.5��4.5Сʱ��������3.5Сʱ���ij���ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com