Question

【题目】在四边形ABCD中，对角线AC与BD交于点O，E是OC上任意一点，AG⊥BE于点G，交直线BD于点F．

（1）如图1，若四边形ABCD是正方形，判断AF与BE的数量关系：AF与BE的数量关系是 ；

（2）如图2，若四边形ABCD是菱形，∠ABC=120°，求的值；

（3）如图3，若四边形ABCD中，AC⊥BD，∠ABC=α，∠DBC=β，请你补全图形，并直接写出：= （用含α，β的式子表示）．

Answer 1

【答案】（1）AF=BE（2）（3）tan（α﹣β）

【解析】

试题分析：（1）根据正方形的性质和全等三角形的性质即可得到结论；

（2）根据四边形ABCD是菱形和∠ABC=120°，推出AC⊥BD，∠ABO=60°，根据余角的性质得到∠AFO=∠BEA，又因为∠AOF=∠BOE=90°，推出三角形相似，即可得到结论；

（3）根据垂直的定义得到∠AGB=∠AOB=90°，推出A，G，B，O四点共圆，根据圆内接四边形的性质得到∠GAO=∠GAO，推出△AOF∽△BOE，即可得到结论．

解：（1）AF=BE；

∵四边形ABCD是正方形，

∴∠AOB=∠BOC=90°，AO=BO，

∵AG⊥BE，∠AFO=∠BFG，

∴∠FAO=∠FBG，

在△AFO与△BFO中，

，

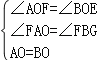∴△AFO≌△BFO，

∴AF=BE；

故答案为：AF=BE；

（2）∵四边形ABCD是菱形，∠ABC=120°，

∴AC⊥BD，∠ABO=60°，

∴∠FAO+∠AFO=90°，

∵AG⊥BE，

∴∠EAG+∠BEA=90°，

∴∠AFO=∠BEA，

又∵∠AOF=∠BOE=90°，

∴△AOF∽△BOE，

∴=，

∵∠ABO=60°，AC⊥BD，

∴=tan60°=，

∴=；

（3）如图3，∵AG⊥BE，AC⊥BD，

∴∠AGB=∠AOB=90°，

∴A，G，B，O四点共圆，

∴∠GAO=∠GAO，

∴∠AOF=∠BOE=90°，

∴△AOF∽△BOE，

∴=，

∵∠ABO=∠ABC﹣∠OBC=α﹣β，AC⊥BD，

∴=tan（α﹣β），

∴=tan（α﹣β）．

故答案为：tan（α﹣β）．