【题目】在平面直角坐标系XOY中，有A(3 , 2) ,B (－1 ,－4 )，P是X轴上的一点，Q是Y轴上的一点，若以点A,B,P,Q四个点为顶点的四边形是平行四边形，则Q点的坐标是______．
【答案】（0，﹣6）或（0，﹣2）或（0，6）．
【解析】试题分析：如图，当AB为边，①当四边形ABQ2P2是平行四边形，所以AB=P2Q2，AP2=BQ2，②当四边形QPBA是平行四边形，所以AB=PQ，QA=PB，当AB为对角线，即当四边形P1AQ1B是平行四边形，所以AP1=Q1B，AQ1=BP1，结合图形分别得出即可．
解：如图所示，
当AB为边，①即当四边形ABQ2P2是平行四边形，所以AB=P2Q2，AP2=BQ2，
∴Q2点的坐标是：（0，﹣6），
②当四边形QPBA是平行四边形，所以AB=PQ，QA=PB，
∴Q点的坐标是：（0，6），
当AB为对角线，即当四边形P1AQ1B是平行四边形，所以AP1=Q1B，
AQ1=BP1，
∴Q1点的坐标是：（0，﹣2）．
故答案为：（0，﹣6）或（0，﹣2）或（0，6）．
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC．过点C作CE⊥DB，垂足为E，直线AB与CE相交于F点．
（1）求证：CF为⊙O的切线；
（2）若⊙O的半径为
cm，弦BD的长为3cm，求CF的长．
考点：切线的判定．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形ABCD中，对角线AC与BD交于点O，E是OC上任意一点，AG⊥BE于点G，交直线BD于点F．
（1）如图1，若四边形ABCD是正方形，判断AF与BE的数量关系：AF与BE的数量关系是 ；
（2）如图2，若四边形ABCD是菱形，∠ABC=120°，求
的值；
（3）如图3，若四边形ABCD中，AC⊥BD，∠ABC=α，∠DBC=β，请你补全图形，并直接写出：= （用含α，β的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市为提倡节约用水，采取分段收费．若每户每月用水不超过20m3，每立方米收费2元；若用水超过20m3，超过部分每立方米加收1元．小明家5月份交水费64元，则他家该月用水 m3．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下列填空．如右图,已知AD⊥BC,EF⊥BC,∠1=∠2. 求证: DG∥BA.
证明：∵AD⊥BC,EF⊥BC（已知）
∴∠EFB=∠ADB=90° ( )
∴ ∥ ( )
∴∠1=∠BAD ( )
又∵∠1=∠2 （已知）
∴ （等量代换）
∴DG∥BA. ( )
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，AD=8，BC=16，点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B运动，点P停止运动时，点Q也随之停止运动，设运动时间为t秒．
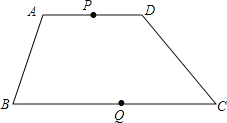
（1）当t为多少时，以点ABQD为顶点的四边形是平行四边形？
（2）当t为多少时，以点ABQP为顶点的四边形是平行四边形？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com