
【题目】甲、乙两人玩摸球游戏,从放有足够多球的箱子中摸球,规定每人最多两种取法,甲每次摸4个或(3-k)个,乙每次摸5个或(5-k)个(k是常数,且0<k<3);经统计,甲共摸了16次,乙共摸了17次,并且乙至少摸了两次5个球,最终两人所摸出的球的总个数恰好相等,那么箱子中至少有球__________个.
【答案】110
【解析】设甲取了x次4个球,取了(16-x)次(3-k)个球,乙取了y次5个球,取了(17-y)次(5-k)个球,依题意k=1,2,当k=1时,甲总共取球的个数为4x+2(16-x)=2x+32,乙总共取球的个数为5y+4(17-y)=y+68,当k=2时,甲总共取球的个数为4x+(16-x)=3x+16,乙总共取球的个数为5y+3(17-y)=2y+51,根据最终两人所摸出的球的总个数恰好相等可得:①2x+32=y+68,即y=2x-34,由x≤16,2≤y≤17且x、y为正整数,不合题意,舍去;②2x+32=2y+51,即2x+2y=19,因x≤16,2≤y≤17且x、y为正整数,不合题意,舍去;③3x+16=y+68,即y=3x-52,因x≤16,2≤y≤17且x、y为正整数,不合题意,舍去;④3x+16=2y+51,即![]() ,因x≤16,2≤y≤17且x、y为正整数,可得x=13,y=2或x=15,y=5;所以当x=13,y=2,球的个数为3×13+16+2×2+51=110个;当x=15,y=5,球的个数为3×15+16+2×5+51=122个,所以箱子中至少有球110个.
,因x≤16,2≤y≤17且x、y为正整数,可得x=13,y=2或x=15,y=5;所以当x=13,y=2,球的个数为3×13+16+2×2+51=110个;当x=15,y=5,球的个数为3×15+16+2×5+51=122个,所以箱子中至少有球110个.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
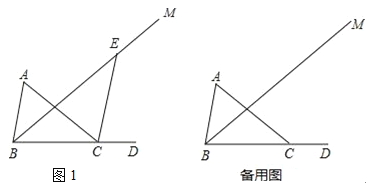
【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市少体校为了从甲、乙两名运动员中选出一名运动员参加省运动会百米比赛,组织了选拔测试,分别对两人进行了五次测试,成绩(单位:秒)以及平均数、方差如表:
甲 | 13 | 13 | 14 | 16 | 18 | x | S |
乙 | 14 | 14 | 15 | 15 | 16 | x | S |
学校决定派乙运动员参加比赛,理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=![]() ∠CGE.其中正确的结论是( )
∠CGE.其中正确的结论是( )
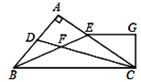
A. ①③ B. ②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师提出了一个问题:
如图1,A、B两点被池塘隔开,在AB外选一点,连接AC和BC,怎样测出A、B两点的距离?

【活动探究】学生以小组展开讨论,总结出以下方法:
(1)如图2,选取点C,使AC=BC=a,∠C=60°;
(2)如图3,选取点C,使AC=BC=b,∠C=90°;
(3)如图4,选取点C,连接AC,BC,然后取AC、BC的中点D、E,量得DE=c…
【活动总结】
(1)请根据上述三种方法,依次写出A、B两点的距离.(用含字母的代数式表示)并写出方法(3)所根据的定理.
AB= ,AB= ![]() b ,AB= .
b ,AB= .
定理: .
(2)请你再设计一种测量方法,(图5)画出图形,简要说明过程及结果即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
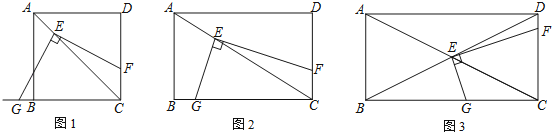
【题目】(1)如图1,将直角的顶点E放在正方形ABCD的对角线AC上,使角的一边交CD于点F,另一边交CB或其延长线于点G,求证:EF=EG;
(2)如图2,将(1)中的“正方形ABCD”改成“矩形ABCD”,其他条件不变.若AB=m,BC=n,试求![]() 的值;
的值;
(3)如图3,将直角顶点E放在矩形ABCD的对角线交点,EF、EG分别交CD与CB于点F、G,且EC平分∠FEG.若AB=2,BC=4,求EG、EF的长.
考点:四边形综合题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)若⊙O的半径为![]() cm,弦BD的长为3cm,求CF的长.
cm,弦BD的长为3cm,求CF的长.

考点:切线的判定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交直线BD于点F.

(1)如图1,若四边形ABCD是正方形,判断AF与BE的数量关系:AF与BE的数量关系是 ;
(2)如图2,若四边形ABCD是菱形,∠ABC=120°,求![]() 的值;
的值;
(3)如图3,若四边形ABCD中,AC⊥BD,∠ABC=α,∠DBC=β,请你补全图形,并直接写出:![]() = (用含α,β的式子表示).
= (用含α,β的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com