
����Ŀ����ͼ��С��վ�ڽ���ij�t��̨DE�Ķ���D������ý����ϵ��洬A�ĸ���Ϊ40�������t��̨DE��ֱ�ڽ��棬���ĸ߶�Ϊ3�ף�CE��2�ף�CEƽ���ڽ���AB��ӭˮ��BC���¶�i��1��0.75���³�BC��10�ף�
���ο����ݣ�sin40���0.64��cos40���0.77��tan40���0.84��cot40���1.19��
��1����t��̨DE�Ķ���D������AB�ľ��룻
��2�����洬A��ӭˮ��BC�ĵ�B�ľ��룮���������һλС����
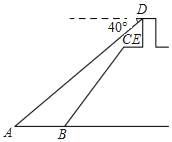
���𰸡���1���t��̨DE�Ķ���D������AB�ľ���Ϊ11�ף�2���洬A��ӭˮ��BC�ĵ�B�ľ���Ϊ5.1��
��������
��1���ӳ�DE��AB�ڵ�F������C��CG��AB������Ϊ��G�������¶ȱ�ʾ��CG��BG�ij�����������𰸣�
��2����Rt��ADF�У�����cotA��![]() ���ó�AF�ij��������ó��𰸣�
���ó�AF�ij��������ó��𰸣�
��1���ӳ�DE��AB�ڵ�F������C��CG��AB������Ϊ��G��

�������֪CE��GF��2��CG��EF
��Rt��BCG����BGC��90����
��i��![]() ��
��
��CG��4k��BG��3k����BC��![]() =5k��10��
=5k��10��
��k��2��
��BG��6����CG��EF��8��
��DE��3����DF��DE+EF��3+8��11���ף���
�𣺲t��̨DE�Ķ���D������AB�ľ���Ϊ11�ף�
��2��������á�A��40����
��Rt��ADF����DFA��90����
��cotA��![]() ��
��
��![]() ��1.19��
��1.19��
��AF��11��1.19��13.09��m����
��AB��AF��BG��GF��5.09��5.1���ף���
���洬A��ӭˮ��BC�ĵ�B�ľ���Ϊ5.1�ף�


 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��![]() ��������
��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ����
����![]() �ύ��
�ύ��![]() �㣬�����߶���Ϊ
�㣬�����߶���Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ����
����![]() �㣮
�㣮
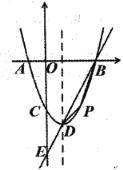
��1���������ߺ�������ʽ��
��2������![]() ��λ��ֱ��
��λ��ֱ��![]() �·��������ϵ�һ���㣬��
�·��������ϵ�һ���㣬��![]() ��
��![]() Ϊ���ڵ�������ƽ���ı���
Ϊ���ڵ�������ƽ���ı���![]() ����ƽ���ı���
����ƽ���ı���![]() ��������ʱ�����ʱƽ���ı���
��������ʱ�����ʱƽ���ı���![]() �����
�����![]() ����
����![]() �����ꣻ
�����ꣻ
��3�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ�����![]() ��
��![]() ��
��![]() ��
��![]() ��������������
��������������![]() ��
��![]() ��
��![]() ��
��![]() ��������ʽ���
��������ʽ���
��1�������ĸ����ĺͣ�
��2�������ĸ�����ѡ������������Ҫ��������м��㣬ʹ�ã�
��������Ľ����С��
���������Ľ�����
��3�������ĸ�����ѡ����������������������ѡ�����֣����һ����ʽ��ʹ����������ûѡ���Ǹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
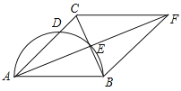
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���İ�Բ��AC�ڵ�D����BC�ڵ�E���ӳ�AE����F��ʹEF=AE������FB��FC��
��1����֤���ı���ABFC�����Σ�
��2����AD=![]() ��BE=1�����Բ�������
��BE=1�����Բ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
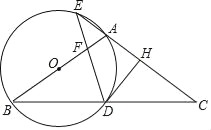
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ����ԲO���ֱ�BC�ڵ�D����CA���ӳ����ڵ�E������D��DH��AC�ڵ�H������DE���߶�OA�ڵ�F��
��1����֤��DH��ԲO�����ߣ�
��2����AΪEH���е㣬��![]() ��ֵ��
��ֵ��
��3����EA=EF=1����ԲO�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8�֣�ij�ֵ��Ӳ�Ʒ��![]() ������������Ʒ�ʹ�Ʒ����֪��������ȡ��һ����ȡ�õIJ�ƷΪ��Ʒ�ĸ���Ϊ
������������Ʒ�ʹ�Ʒ����֪��������ȡ��һ����ȡ�õIJ�ƷΪ��Ʒ�ĸ���Ϊ![]() ��
��
��1��������Ʒ����Ʒ ����
��2�������������ȡ��![]() ���������б�����״ͼ��ȡ��
���������б�����״ͼ��ȡ��![]() ��������Ʒ�ĸ��ʣ�
��������Ʒ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ŷ����Ǵ��ϲ����һ���˶�.�����������С����![]() ����С����
����С����![]() ��������㳡��ˮ ƽ�����Ϸŷ��ݣ���������ڿ���
��������㳡��ˮ ƽ�����Ϸŷ��ݣ���������ڿ��� ![]() ��������һ����ͼ��ʾ. ��ʱ��С�� �ķ�����
��������һ����ͼ��ʾ. ��ʱ��С�� �ķ����� ![]() ��ˮƽ�ߵļн�Ϊ
��ˮƽ�ߵļн�Ϊ ![]() ��С���ķ�����
��С���ķ����� ![]() ��ˮƽ�ߵļн�Ϊ
��ˮƽ�ߵļн�Ϊ ![]() ��С�� ��С��֮��ľ���
��С�� ��С��֮��ľ��� ![]() Ϊ
Ϊ ![]() ��.��֪��
��.��֪�� ![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ,���
,��� ![]() ������ľ���
������ľ��� ![]() Ϊ�����ף��������з����߾���Ϊ�߶Σ�
Ϊ�����ף��������з����߾���Ϊ�߶Σ�![]() �������ȷ��
�������ȷ�� ![]() �ף�
�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
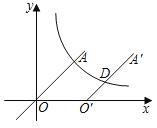
����Ŀ����ͼ������������y��x��ͼ���뷴��������y��![]() ��ͼ���ڵ�һ�����ڵ�A�����߶�OA��x������ƽ��3����λ���ȵõ��߶�O'A'�����е�A���A'��Ӧ����O'A'���е�Dǡ��Ҳ�ڸ÷���������ͼ���ϣ���k��ֵΪ_____��
��ͼ���ڵ�һ�����ڵ�A�����߶�OA��x������ƽ��3����λ���ȵõ��߶�O'A'�����е�A���A'��Ӧ����O'A'���е�Dǡ��Ҳ�ڸ÷���������ͼ���ϣ���k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
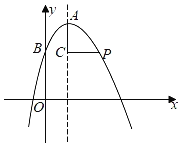
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪�����ߵĶ���ΪA(2��![]() )����������y�ύ�ڵ�B(0��
)����������y�ύ�ڵ�B(0��![]() )����C����Գ�������λ�ڵ�A�·������߶�AC�Ƶ�C��˳ʱ�뷽����ת90�㣬��A�����������ϵĵ�P����
)����C����Գ�������λ�ڵ�A�·������߶�AC�Ƶ�C��˳ʱ�뷽����ת90�㣬��A�����������ϵĵ�P����
(1)�������ߵĽ���ʽ��
(2)���߶�AC�ij���
(3)��������ƽ�ƣ�ʹ�䶥��A�Ƶ�ԭ��O��λ�ã���ʱ��P���ڵ�D��λ�ã������M��y���ϣ�����O��C��D��MΪ������ı��ε����Ϊ8�����M�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com