
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB、FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圆的面积.
,BE=1,求半圆的面积.
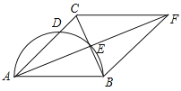
【答案】(1)见解析;(2)半圆的面积是![]()
【解析】
(1)由AB是直径可得∠AEB=90°,根据等腰三角形的性质可得BE=CE,进而可得四边形ABFC是平行四边形,再根据菱形的定义即可证得结论;
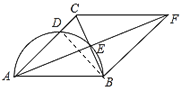
(2)连接![]() ,如图,设
,如图,设![]() ,根据勾股定理可得关于x的方程,解方程即可求出x,进一步即可求出半圆面积.
,根据勾股定理可得关于x的方程,解方程即可求出x,进一步即可求出半圆面积.
(1)证明:∵AB是直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴平行四边形ABFC是菱形;
(2)解:连接![]() ,如图,设
,如图,设![]() ,则AC=x,
,则AC=x,
∵AB是直径,∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
则![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,
∴半圆的面积![]() .
.
答:半圆的面积是![]() .
.


科目:初中数学 来源: 题型:
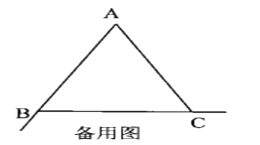
【题目】如图, 已知等边![]() , 点
, 点![]() 在射线
在射线![]() 上(不与
上(不与![]() 重合),连接
重合),连接![]() , 将射线
, 将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() .
.
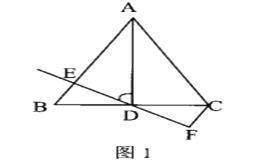
(1)如图1,当点D为线段BC中点时,请直接写出CF,BE,CD三条线段之间的数量;
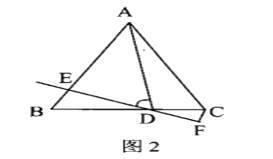
(2)如图2,“点![]() 在线段
在线段![]() 上且不是
上且不是![]() 中点时,
中点时,![]() 中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
(3)若![]() ,当
,当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=2 ![]() ,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
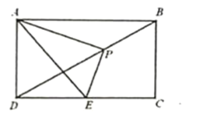
(1)求证:∠PAD=∠PEC;
(2)当点P是BD的中点时,求DE的值;
(3)在点P运动过程中,当DE= ![]() 时,求BP的值.
时,求BP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
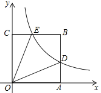
【题目】平面直角坐标系中,正方形OABC如图放置,反比例函数![]() 的图像交AB于点D,交BC于点E,已知A(
的图像交AB于点D,交BC于点E,已知A(![]() ,0),∠DOE=30°,则k的值为( )
,0),∠DOE=30°,则k的值为( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角形纸片的两直角边AC与BC的比为3:4,首先将△ABC如图1所示折叠,使点C落在AB上,折痕为BD,然后将△ABD如图2所示折叠,使点B与点D重合,折痕为EF,则sin∠DEA的值为( )
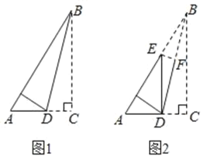
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年第七届世界军人运动会(7thCISMMilitaryWorldGames)于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在一次训练中射击了10次,成绩如图所示.下列结论中不正确的有( )个
①众数是8;②中位数是8;③平均数是8;④方差是1.6.
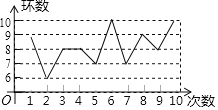
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两座现代化城市,
是两座现代化城市,![]() 是一个古城遗址,
是一个古城遗址,![]() 城在
城在![]() 城的北偏东
城的北偏东![]() ,在
,在![]() 城的北偏西
城的北偏西![]() ,
,![]() 城在
城在![]() 城的正东方向,且
城的正东方向,且![]() 城与
城与![]() 城相距120千米,现在
城相距120千米,现在![]() 、
、![]() 两城市修建一条笔直的高速公路.
两城市修建一条笔直的高速公路.
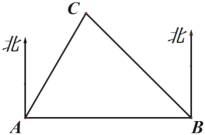
(1)请你计算公路![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)若以![]() 为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路
为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路![]() 会不会穿越这个保护区,并说明理由.
会不会穿越这个保护区,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,点B位于(4,0)、(5,0)之间,与y轴交于点C,对称轴为直线x=2,直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴上方且横坐标小于5,则下列结论:①4a+b+c>0;②a﹣b+c<0;③m(am+b)<4a+2b(其中m为任意实数);④a<﹣1,其中正确的是( )

A.①②③④B.①②③C.①②④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com